【阅读时间】10min 3326words
【阅读内容】通过构造知识联想链条和直观例子回答什么是泰勒级数,为什么需要泰勒级数,泰勒级数干了什么,如何记忆这个公式
本篇博客回答知乎问题怎样更好的理解,并且记忆泰勒展开式? (求点赞^_^)
For me, mathematics is a collection of examples; a theorem is a statement about a collection of examples and the purpose of proving theorems is to classify and explain the examples
John B. Conway
对于我而言,数学就是范例的集合——定理是为了描述范例,证明定理是为了分类并解释范例
约翰·B·康威
在遇到一个生僻的概念或者公式时,确认它的几种不同的表述形式(马甲)是很重要,也就是定义问题:我们到底要了解的东西是什么 & 怎么称呼:
泰勒公式(也叫 泰勒展开式、泰勒多项式)
泰勒级数
它是微积分学下的一个重要概念,与之有关联的有:如泰勒定理,多元泰勒公式,以拉格朗日型余项为代表的各类余项,审敛法,牛顿差值公式(牛顿级数)(列出为了进行树状知识整合和梳理)
什么是泰勒公式
基本定义
数学定义,公式各个部分代表什么含义先说清楚
$$ \begin{align} f(x)_{Taylor} &= \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} \times (x - a)^n \\ &= f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f^{(2)}(a)}{2!}(x-a)^2+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x) \end{align} $$$f^{(n)}(a)$ 表示 $f(x)$ 在第 $n$ 阶导数的表达式,带入一个值 $a$ 计算后得到的结果(注意,它是个值)
$\frac{1}{n!}$ 是一个系数(一个值),每一项都不同,第一项 $\frac{1}{1}$,第二项 $\frac{1}{2!}$ …… 依此类推
$(x-a)^n$ 是一个以 $x$ 为自变量的表达式求和符号去掉展开写即第二行
$R_n(x)$ 是泰勒公式的余项,是 $(x-a)^n$ 的高阶无穷小(此处先不解释,听起来很牛逼,但是跟随例子看完就发现并没有什么玄乎的)
个人粗浅总结,初学者产生记不住的感觉大多数情况下是没有沉下心来想想公式的各部分表示的是什么东西,梳理一下会清晰很多
联想链条
所有的 <内容>➜ 符号都表达【由<内容>联想到】(一种牢固记忆的技巧)
联想链条是为了给你一把一个长期记忆的钥匙,很久不用之后,估计只能记住【泰勒公式】四个字了,如何利用这仅有的信息回忆起具体的理解和内容,除了理解透彻,直观,利用图像外,弄一个联想链条也是不错的方法
首先拆字
【公式】 <什么公式?>➜ 【多项式】(Polynomials),把多项式的一般形式写出来,这应该是非常容易理解的概念,即指数不仅仅为2的抛物线的组合
$$ P_{n}(x) = \sum_{i = 0}^{n} c_ix^i = c_0 + c_1x + c_2x^2 + \cdots + c_nx^n $$【泰勒】<谐音“太乐” ≈ 如果所有小数都能近似成整数那不是太快乐了?> ➜ 近似,获得一个直观理解
- 泰勒公式通过把【任意函数表达式】转换(重写)为【多项式】形式,是一种极其强大的函数近似工具
为什么说它强大呢?
- 多项式非常【友好】,三易,易计算,易求导,易积分
- 几何感觉和计算感觉都很直观,如抛物线和几次方就是底数自己乘自己乘几次
泰勒公式干的事情就是:使用多项式表达式估计(近似) $f(x)$ 在 $x = a$ 附近的值
那么如何近似呢?使用一个例子来加深理解
怎样理解泰勒公式
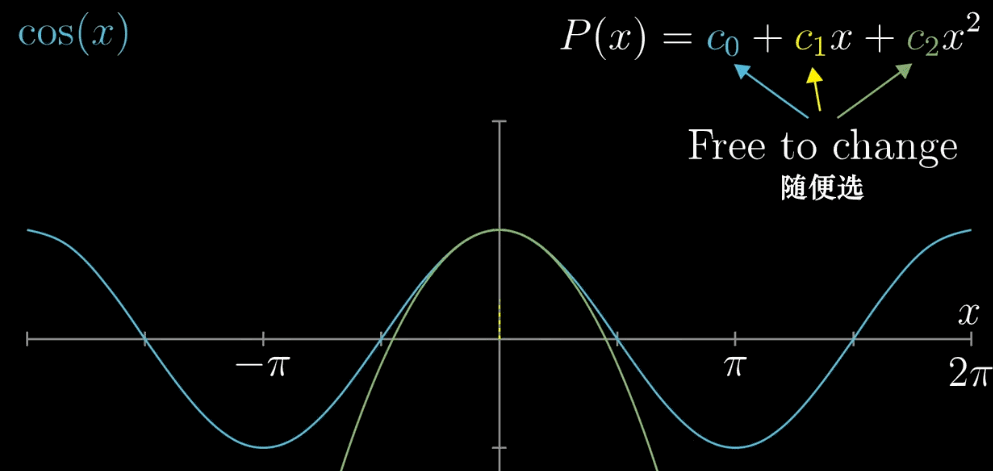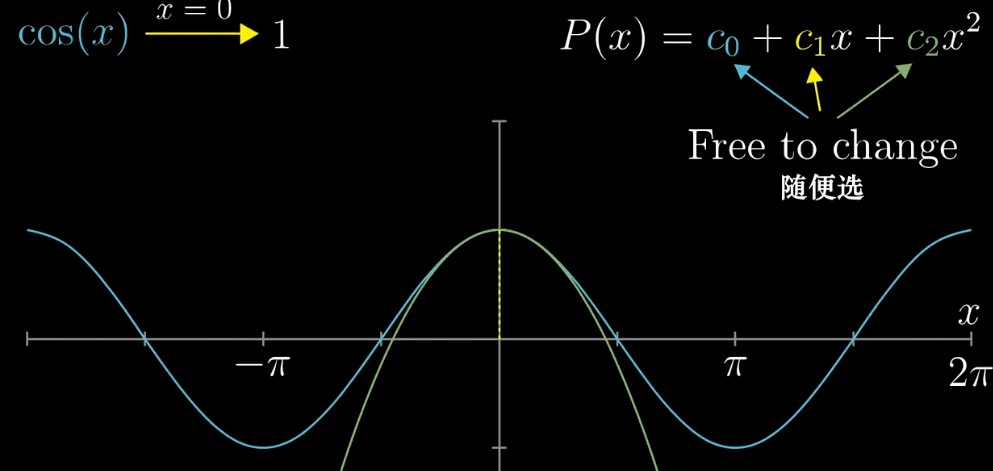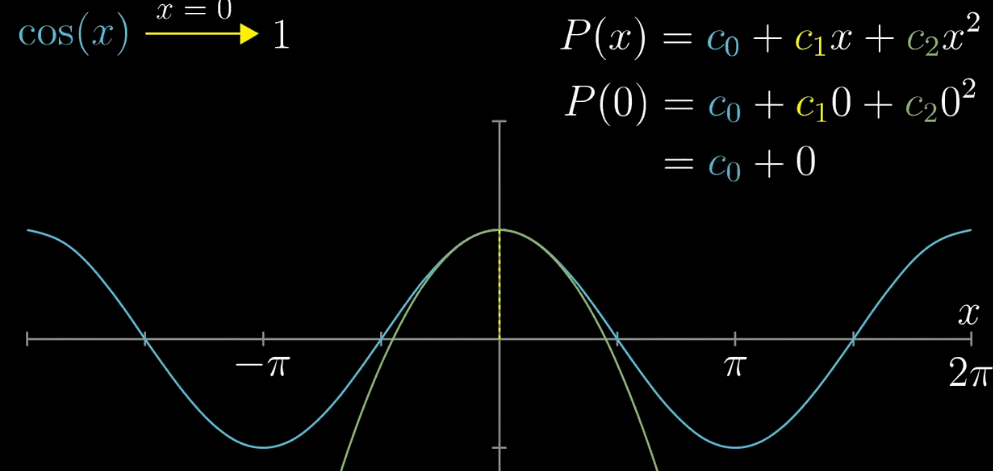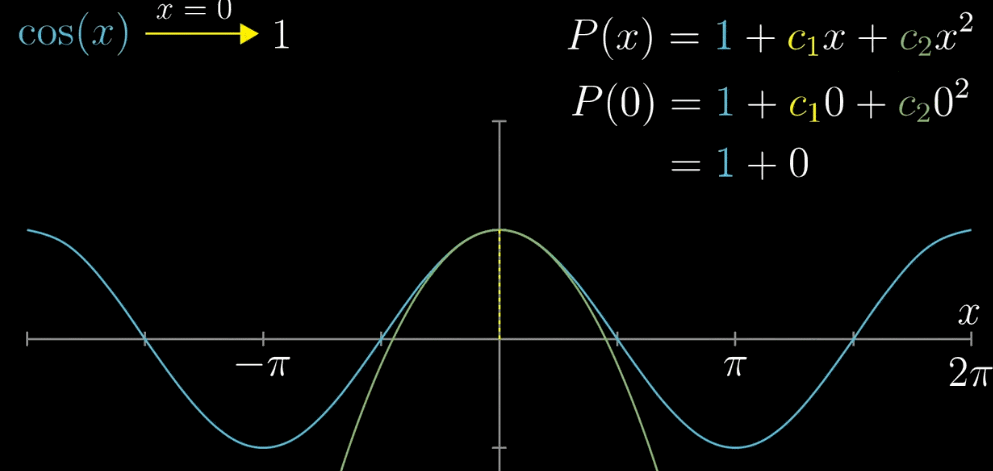
我们要干的事情,就是改变多项式函数 $P(x) = c_0 + c_1x + c_2x^2$ 中 $c_0, c_1, c_2$ 的值
(只有三项是为图个方便)去近似余弦函数 $f(x) = cos(x)$ ,【近似过程】参考下面的动图
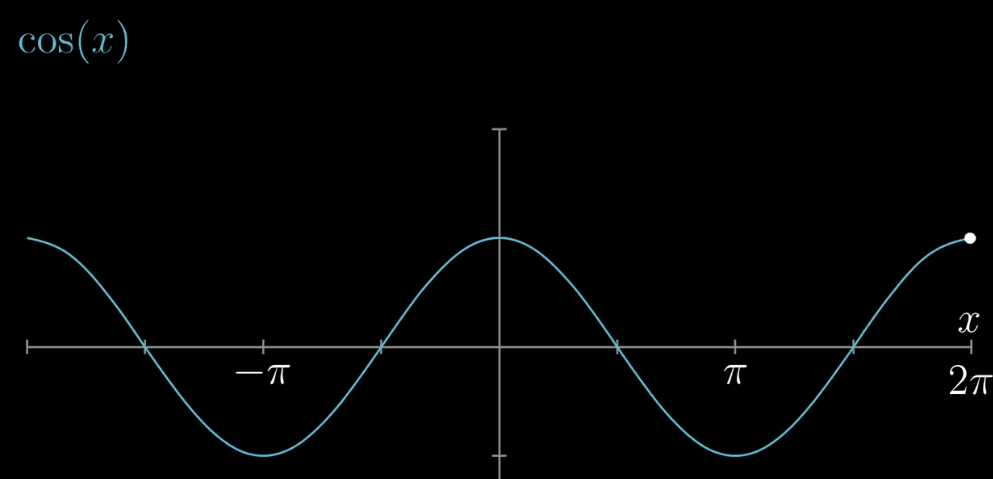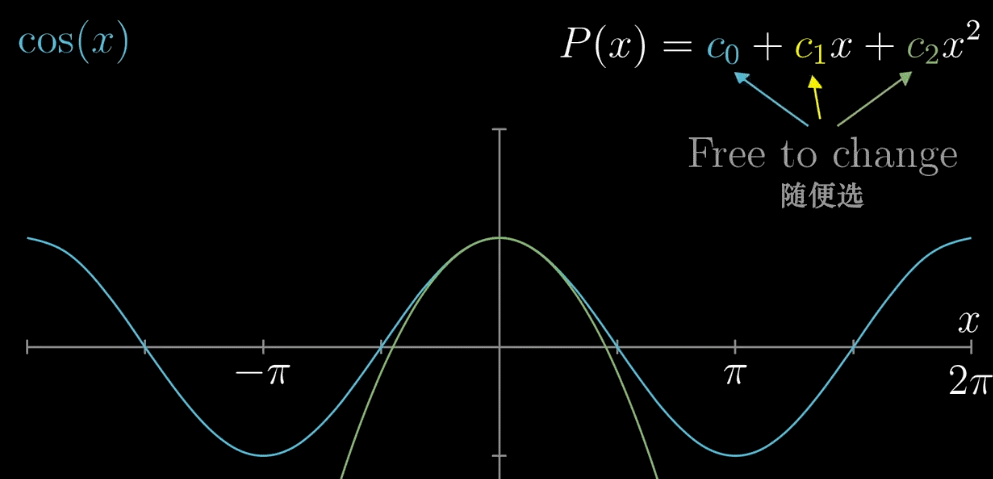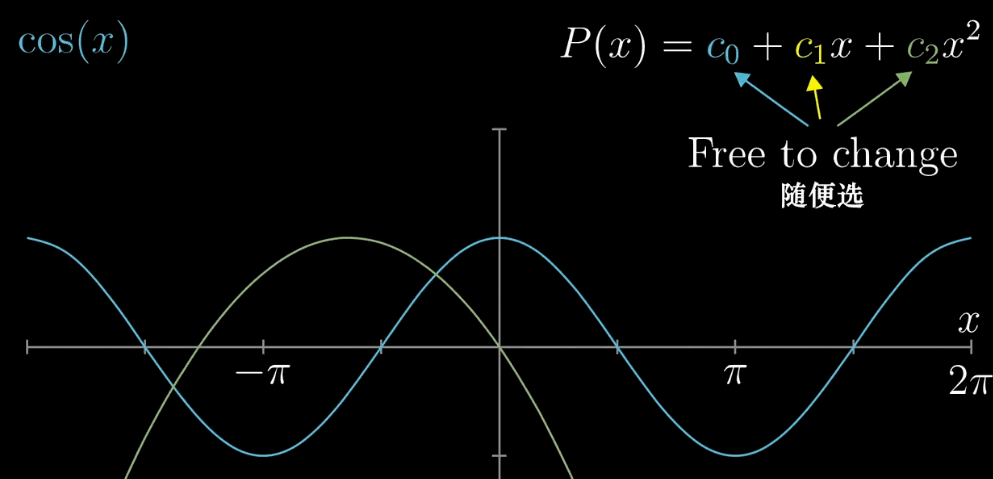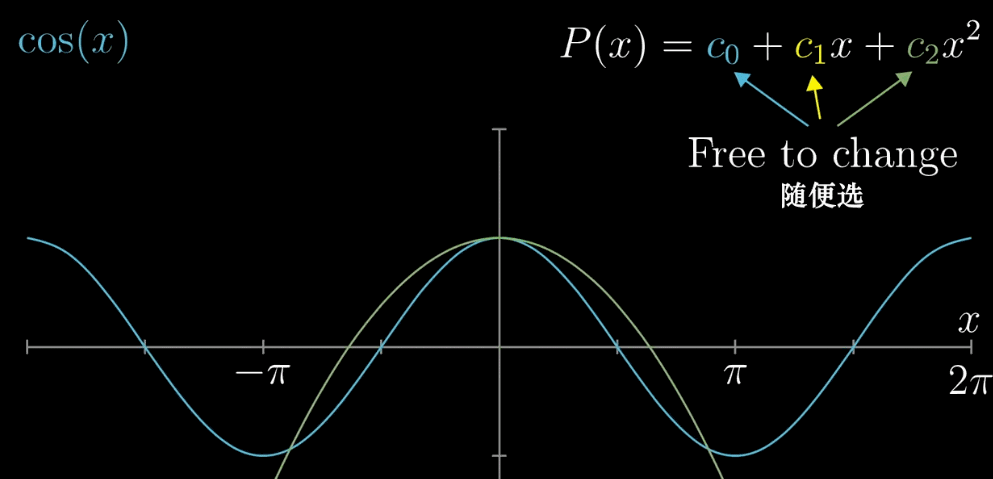
我们需要做的事情(目的)即寻找一条绿色的曲线(多项式的系数 $c_0, c_1, c_2$),在 $x = 0$ 附近(0为上面提到的 $a$)尽可能的与 $f(x) = cos(x)$ 的图像相似(重合)
函数式角度
那如何才能找到这三个参数呢?最为显而易见的做法就是希望在 $x=0$ 的位置,两个表达式的切线尽量相等,切线即斜率,也就是求导,比较抽象,一步一步来可视化一下
近似过程
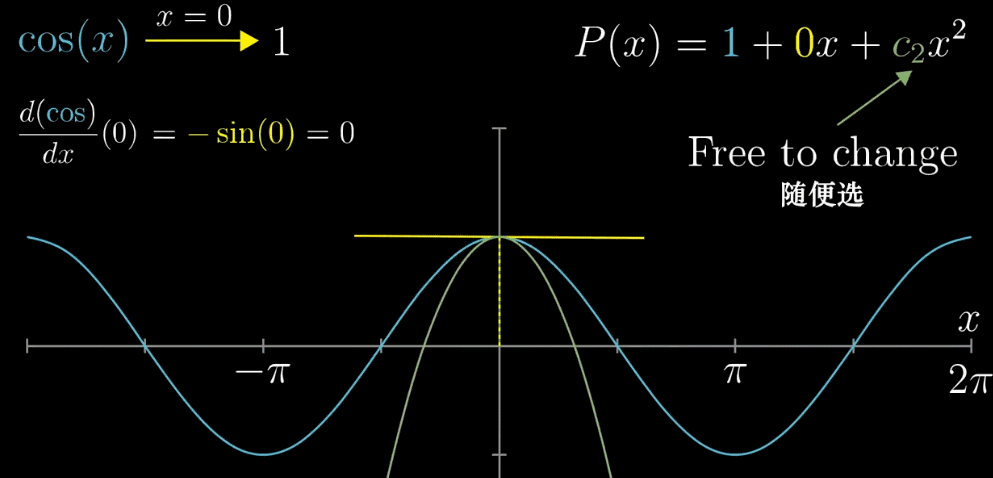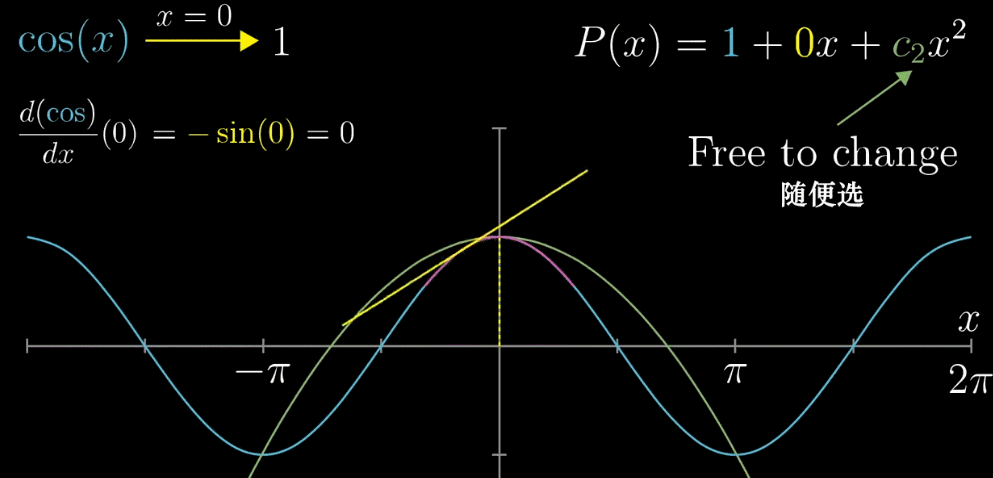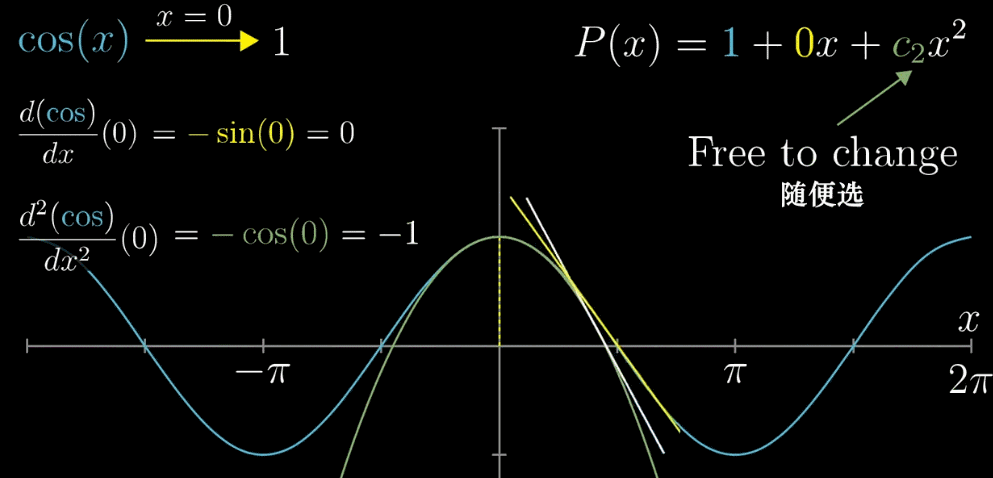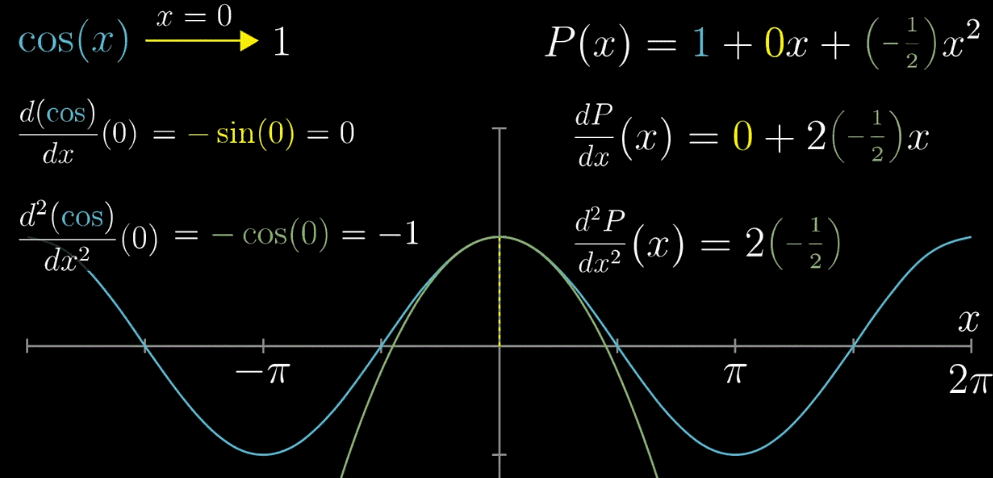
- 【确定 $c_0$】$x=0$ 带入公式,令 $cos(x) = 1$ ,同理对 $P(x)$ 可以得到 $c_0=1$
【确定 $c_1$】容易观察到,如果对 $P(x)$ 求导就可以把 $c_1$ 前的自变量去掉。并且,$x=0$ 处 $P(x)$ 已经固定为1,为了更进一步的相似,如果我们让 $x=0$ 处的 $f(x)$ 和 $P(x)$ 的切线斜率也相同不就更近似了?(两种思考模式我觉得都可以) 求导之后可以的到 $c_1 = 0$
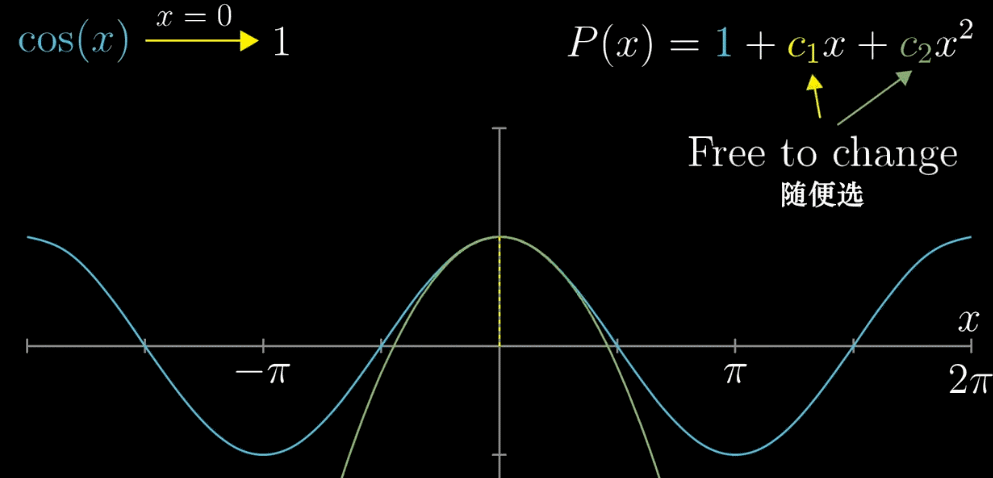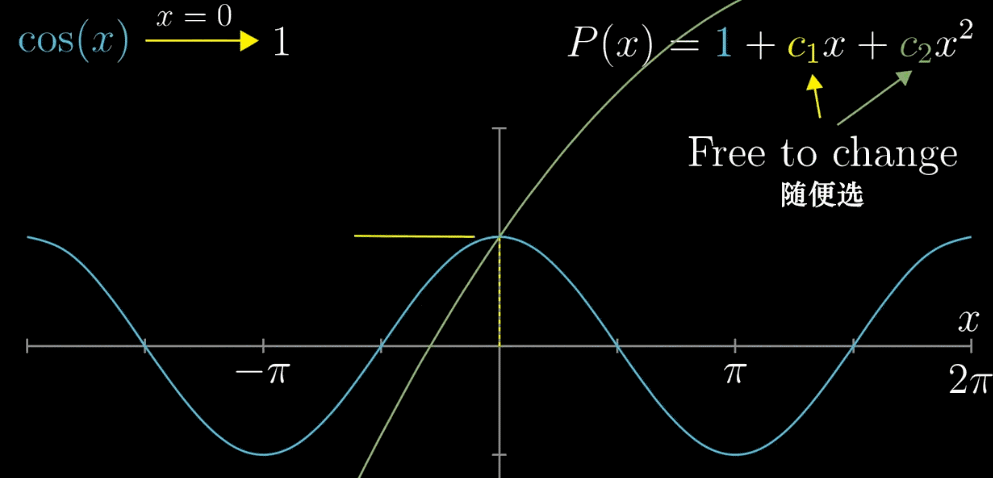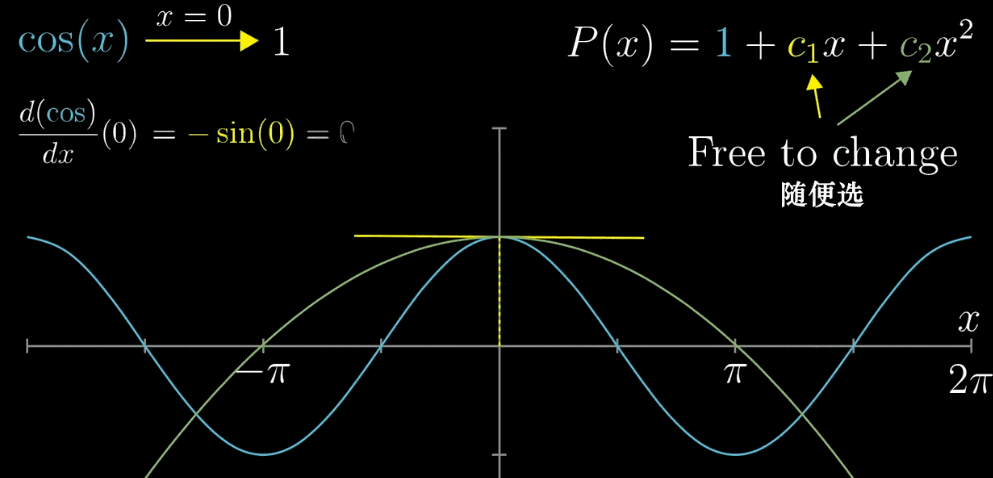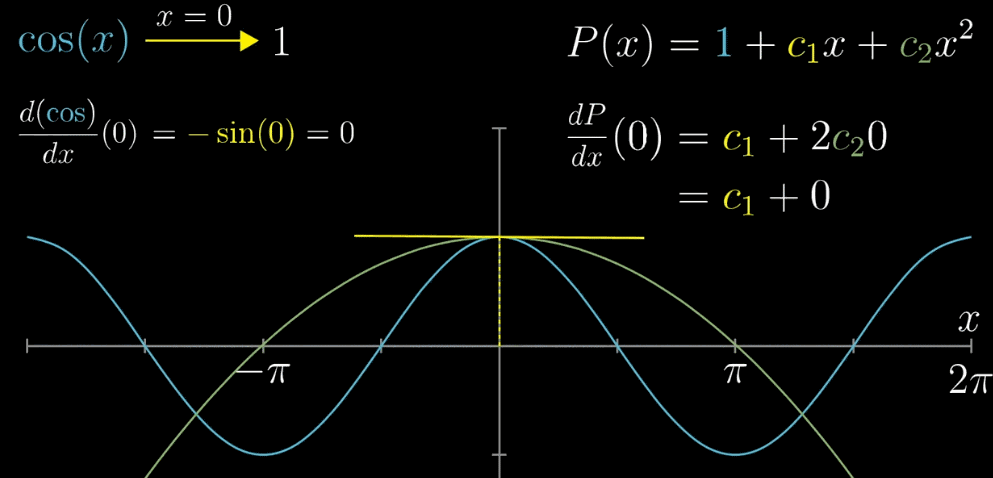
【确定 $c_2$】现在我们已经确定两个值,那么绿色曲线就只能如下图一样移动(固定了 $x=0$ 的函数值和 $x=0$ 处的斜率 ),为了更接近相似的目标,我们希望斜率在变化的过程中,速度也是近似的(滑动的白色和黄色直线)。求二次导数,斜率的变化率相等,确定 $c_2 = -\frac{1}{2}$
此时得到表达式 $P(x) = 1 - \frac{1}{2}x^2$ ,检测一下近似度如何?$cos(0.1) \approx 1 - \frac{1}{2}(0.1)^2 = 0.995$ 同时计算器 $cos(0.1) = 0.9950042$ ,其实只取前几项的多项式已经在 $x=a$ 附近的近似这一要求上有很好的效果了
为什么这个【近似过程】写的这么详细,是为了在过程中体会两个关键点
为什么使用多项式来近似
因为多项式的求导法则可以控制变量,消去低次项,使得 $x=a$ 未知的 $c_n$ 容易确定,在之前的例子里,如下图所示
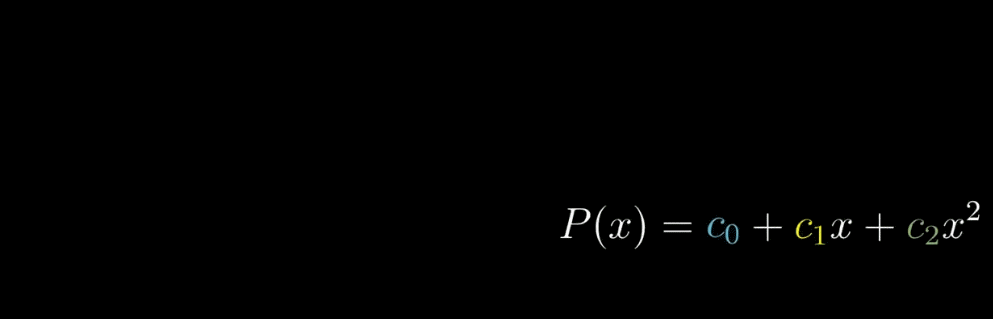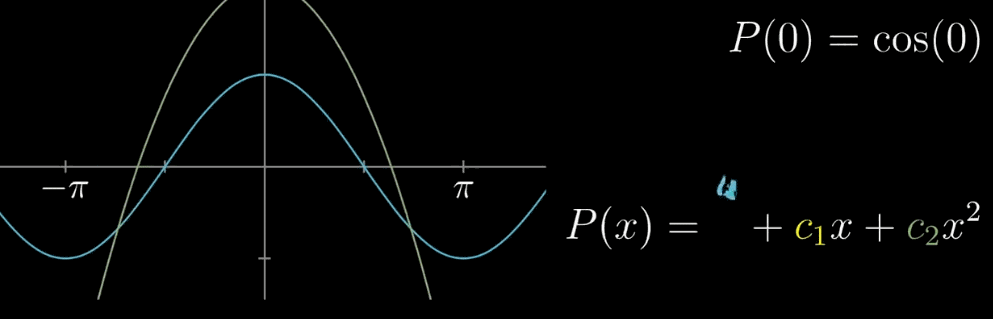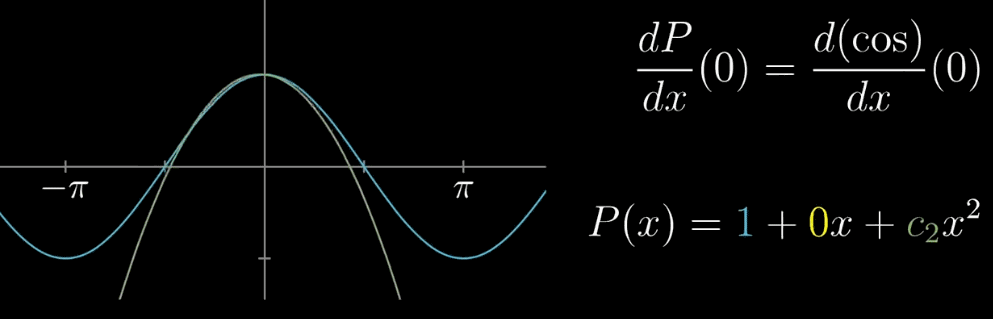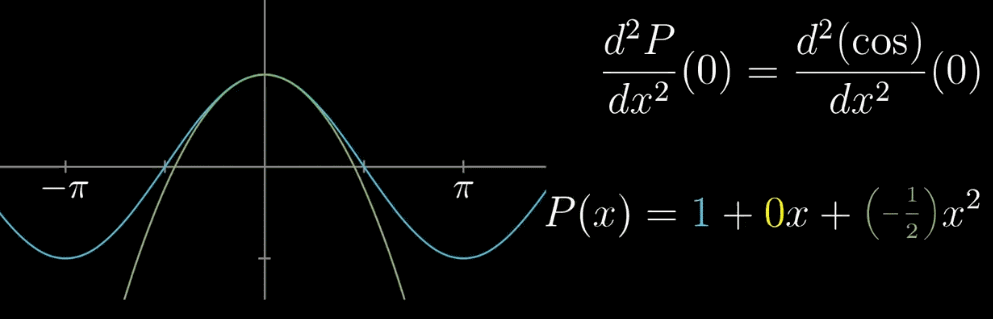
$c_0$ 确保了 $x=0$ 时相等,$c_1$ 确保了 $x=0$ 时的斜率相等,$c_2$ 确保了 $x=0$ 时斜率的变化率相等,或者说,随着多项式幂次变高,这种近似就越精确
为什么有个系数 $\frac{1}{n!}$
阶层系数是由一次一次的求导产生的。我们再把项数加两个,参看下图,直观的感受一个 $n!$ 的诞生
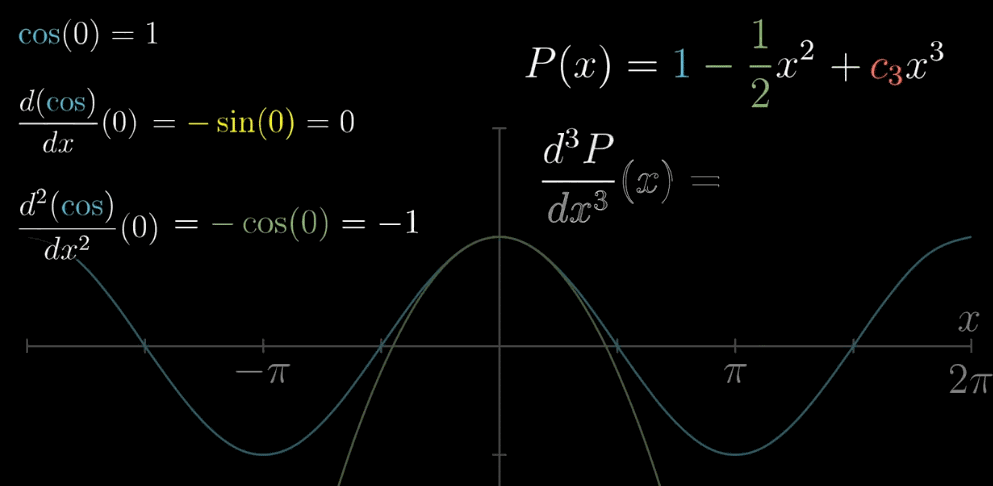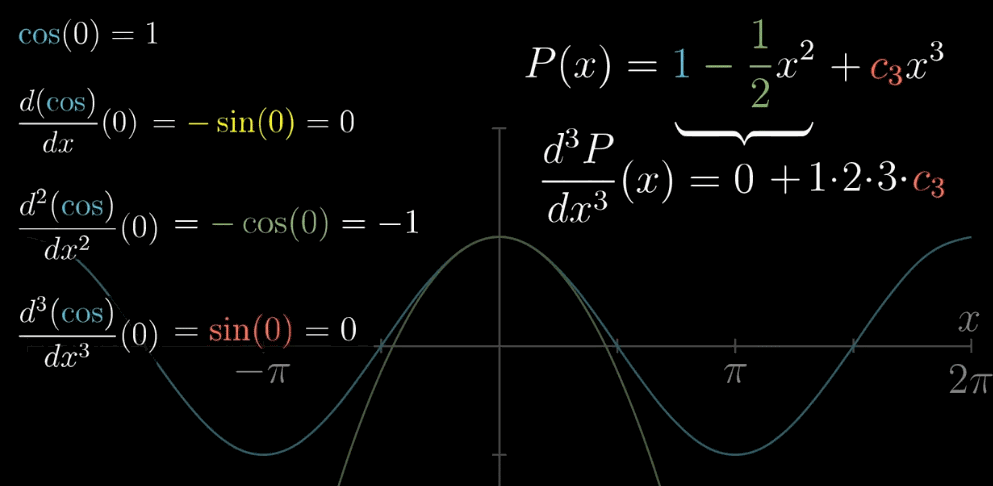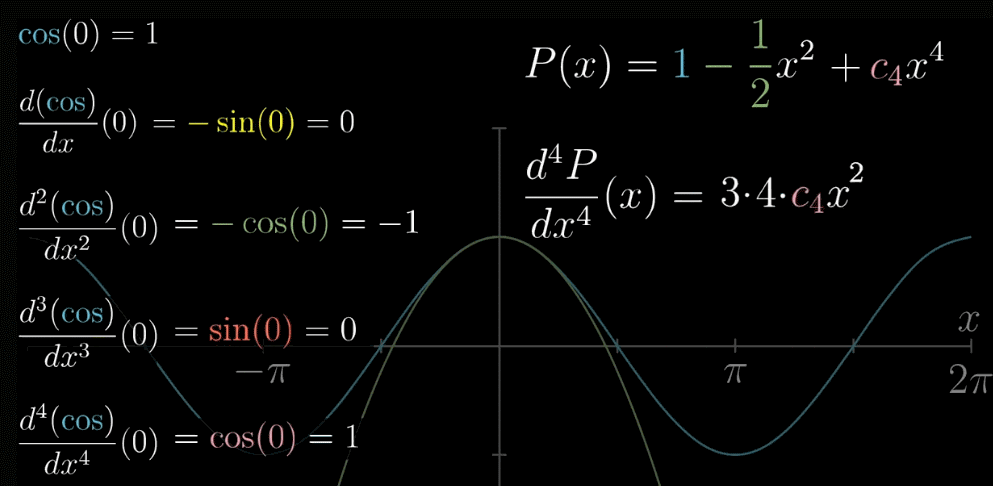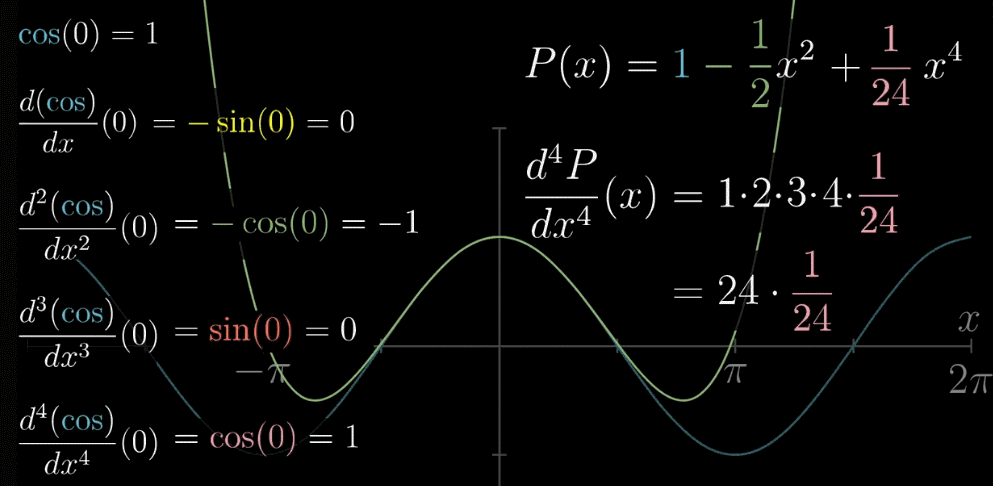
首先,低次项会变为0,这样可以很方便的通过计算 $f(x)$ 的 $n$ 次求导的表达式,带入 $x=a$ 即可得到 $c_n$ 的值,阶层其实是多次求导的系数
函数角度总结
其实,某一点处的导数值信息 $\iff$ 那一点附近的函数值信息 这个直观感觉,是很重要的
首先,对于 $cos(x)$ 这个具体例子,把 $x=0$ 位置的多阶导数求出,再使用多项式进行近似,使用的项越多,得到的近似就越准确,参看下面动图
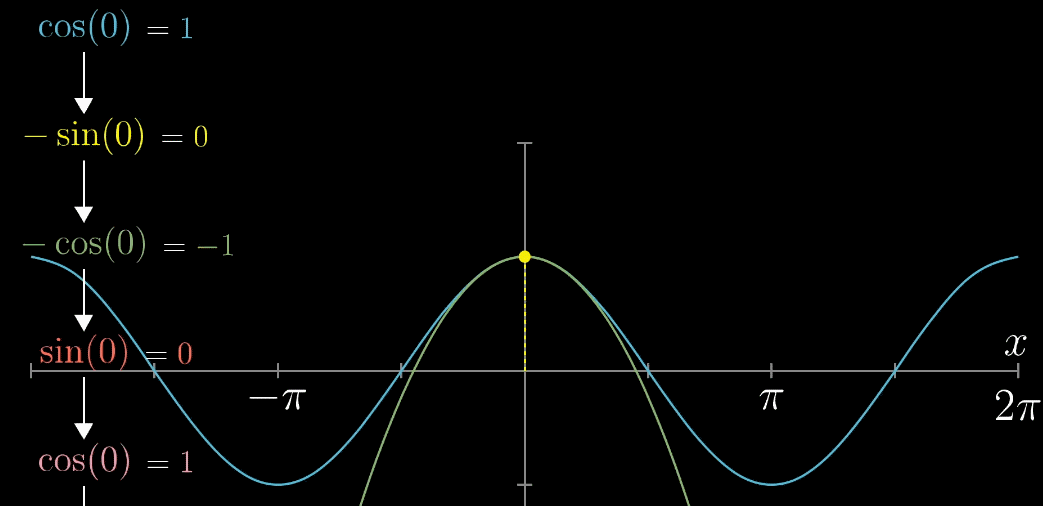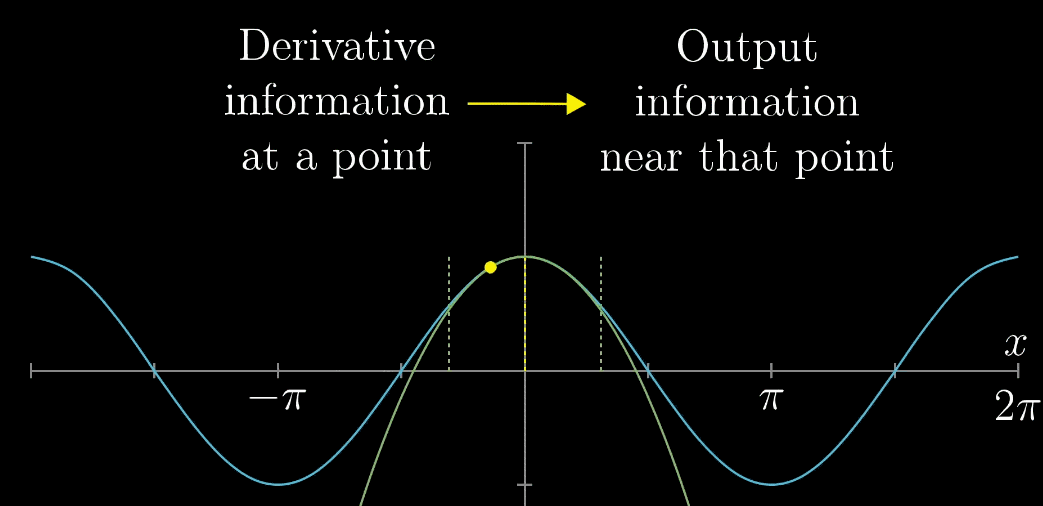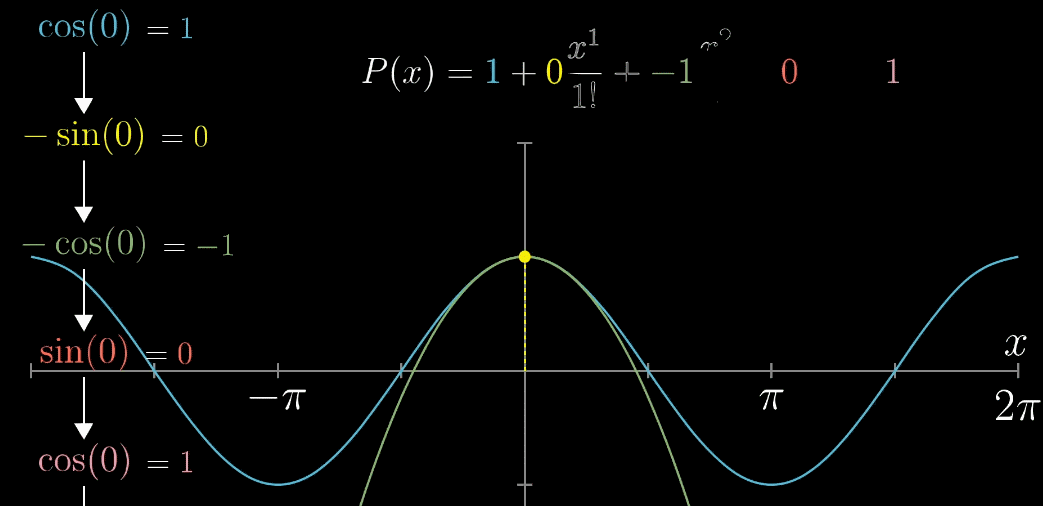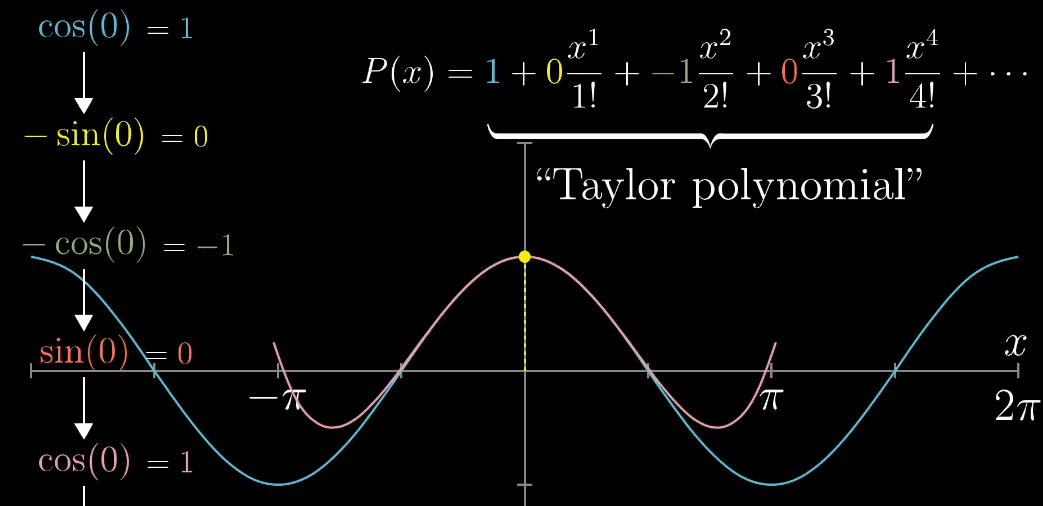
推广到一般函数 $f(x)$ ,下列动图描述了随着项的增加,$x=0$ 附近的越来越准确
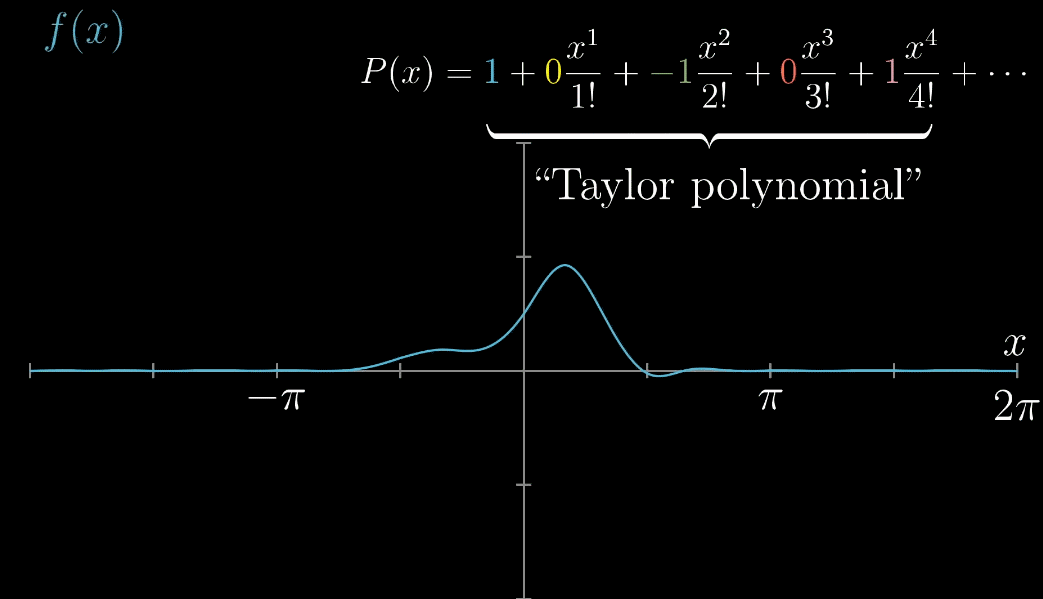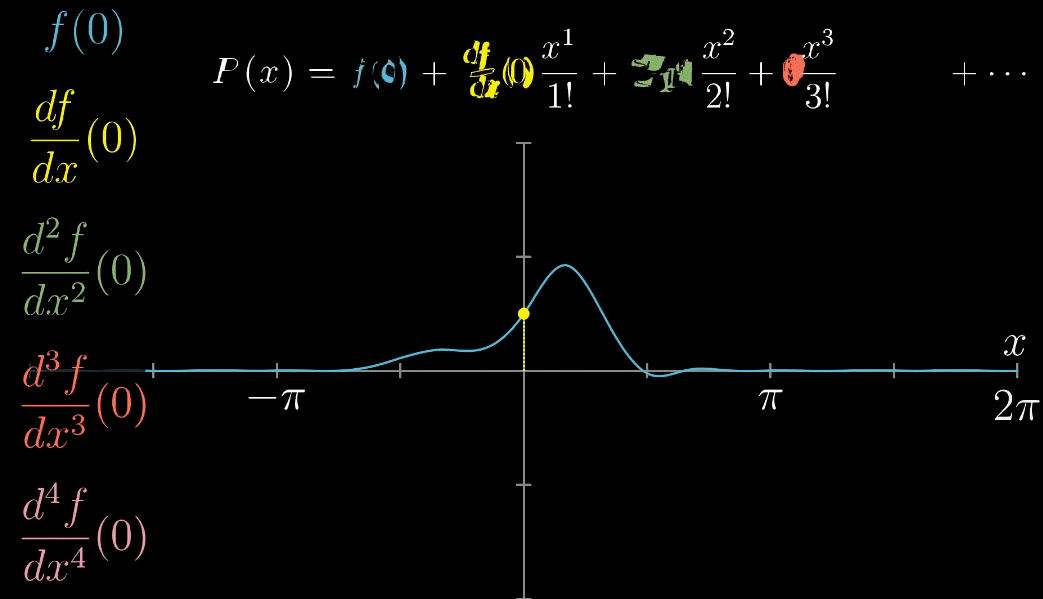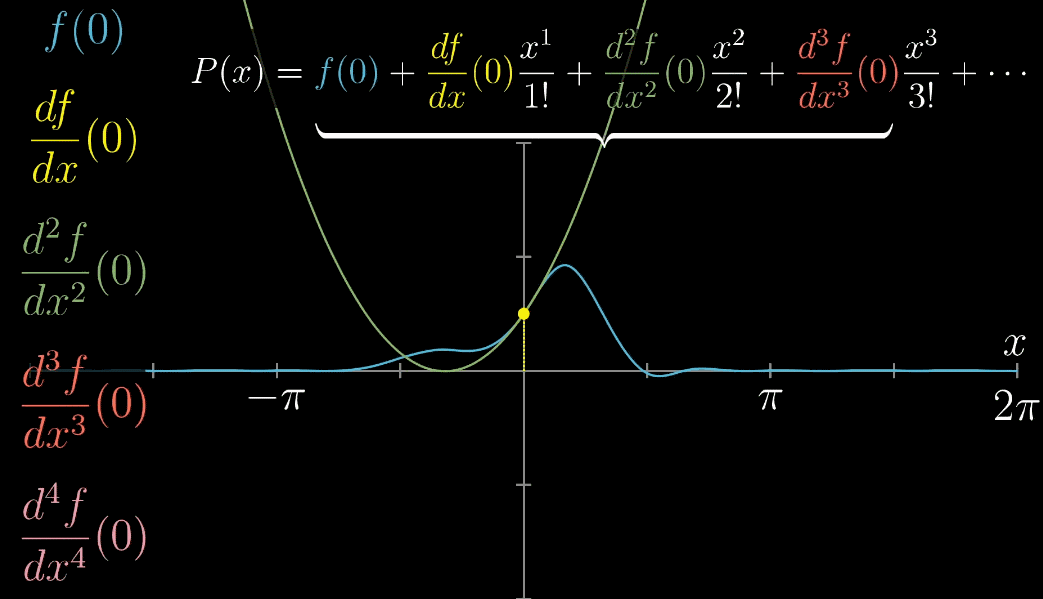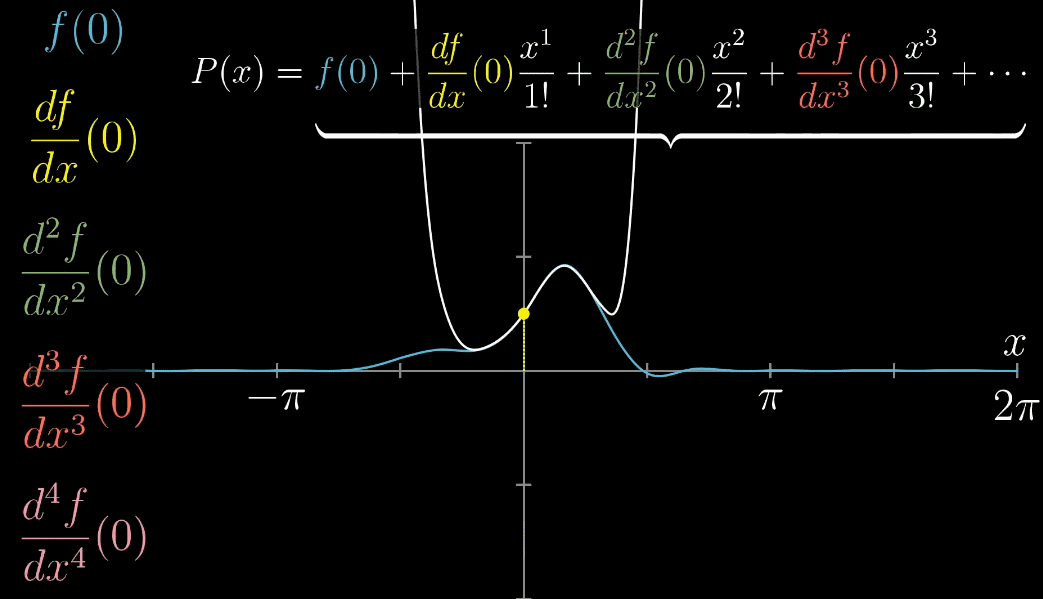
最后,推广到 $x=a$ 的情形,完全推导出泰勒展开式的一般形式,如下列动图所示
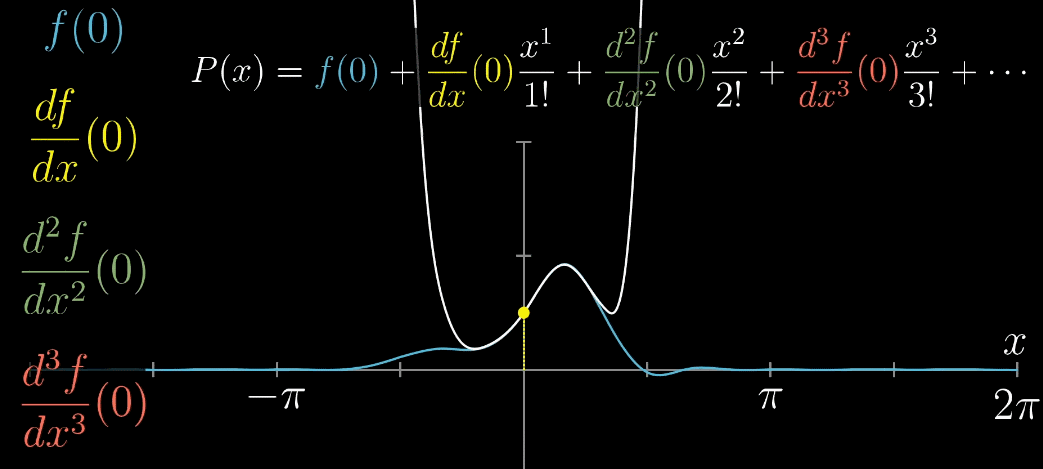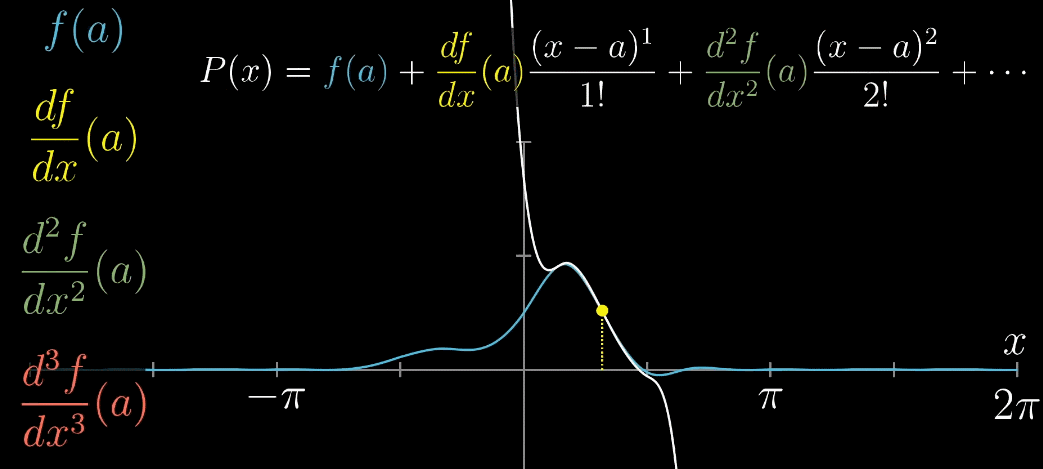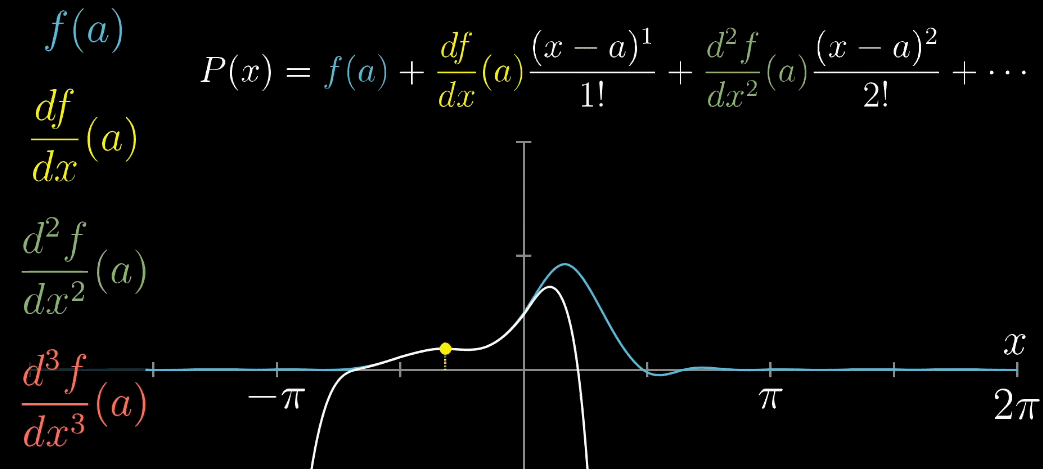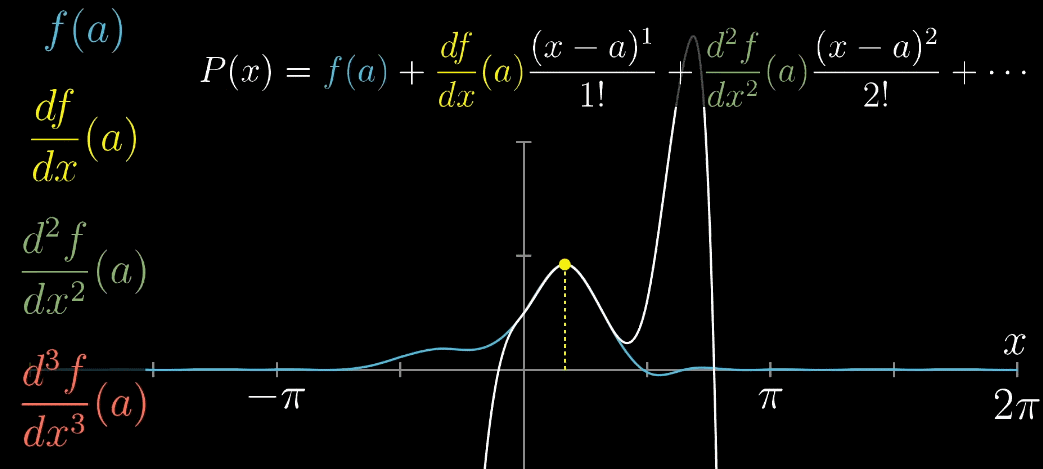
几何角度
首先定义一个函数表示求下列图像中函数图像中填满部分的面积,函数为 $f(x)$ ,面积函数为 $f_{area}(x)$ ,而围成面积区域的曲线即为面积函数的导数 $\frac{df_{area}}{dx}(x)$ (至于为什么是这样,有一个牛逼的名字叫做,微积分基本定理: $\int_{a}^{b}f(t)dt = F(b)-F(a)$ ,没那么玄乎,在3B1B的另一个视频内讲解的相当直观。博主也可以写那一期的博客,如果要求的读者多的话),如下图所示
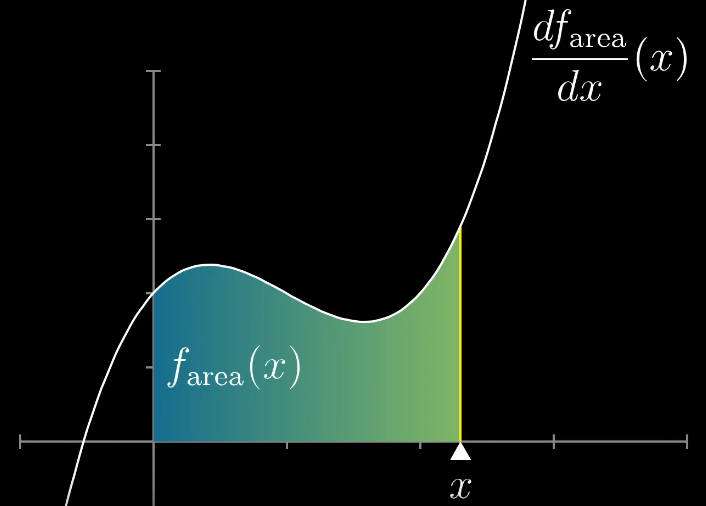
定义一个这样的场景是为了计算这样一件事(如下图所示):假设我们知道了 $f(a)$ 点的面积,往右扩展很小的距离 $dx$ 要算出新部分的面积(左边绿色已知 + 黄色矩形 + 红色三角形),公式会是什么样的呢?
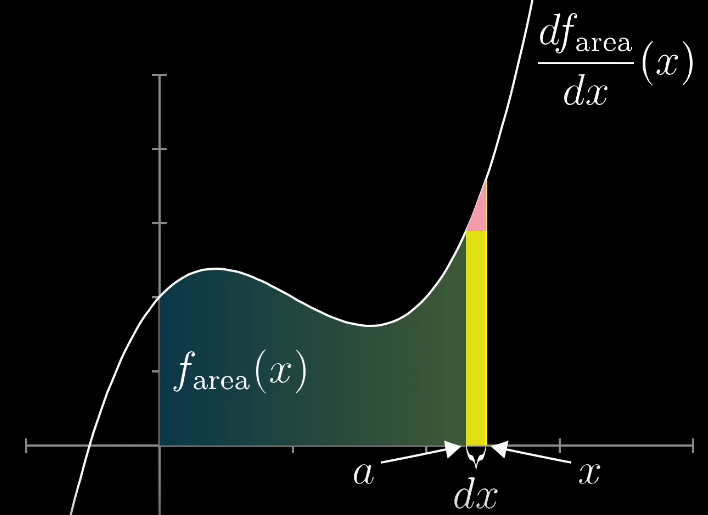
设 $dx$ 开始点为 $a$,终点为 $x$ ,则可以得到
- 【黄色矩形】底边为 $x-a$ ;高为 $\frac{df_{area}}{dx}(a)$ ;
- 【红色三角形】底边为 $x-a$;高的计算稍微麻烦,首先,斜边的斜率是 $\frac{df_{area}}{dx}(x)$ 函数的导数在 $x=a$ 时的函数值(算斜率,求导数即可),而斜率 $k = \frac{y}{x}$ ,所以得到高为 $\frac{d^2f_{area}}{dx^2}(a) \times (x-a)$ (前部分是斜率,后半部分是 $x$ ,需要求的是 $y$ 也是高)
- 【计算总面积】如下图和公式所示
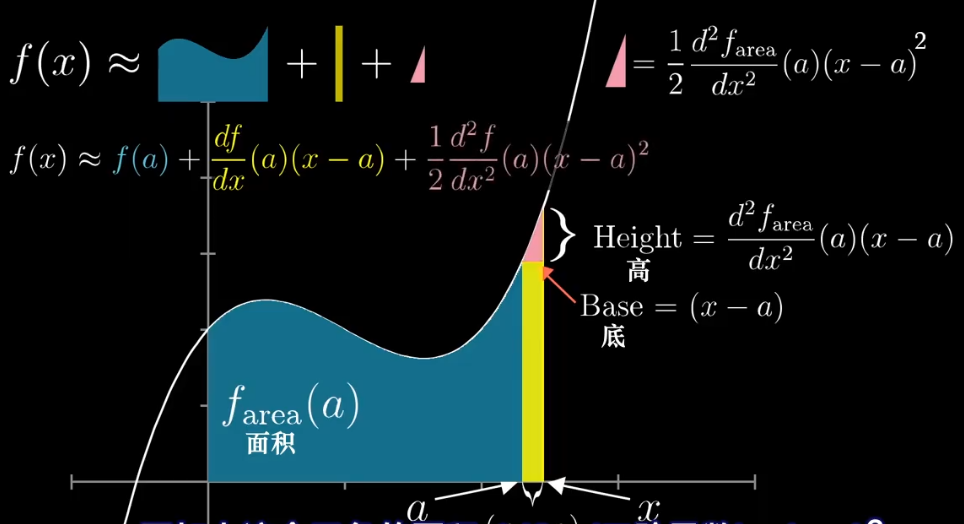
这个公式为啥这么眼熟呢?其实明显就是泰勒展开式的前3项,如果你还要打破沙锅问到底,第4项呢?你可以放大红色三角形,把函数曲线和面积之间的空白部分再次用多个更小的三角形填补,在积分工具的帮助下,可以得到三次项
从几何角度来看,再一次验证了,泰勒公式是近似的 $x=a$ 附近的函数值这一直观理解
余项
我们知道,对泰勒公式来说,并没有办法完全逼近待求函数,所以无论如何到最后都会留一点东西,这剩下的东西不好表达,就全都丢到余项中
可以暂时如此理解,不在此迷惑,如果是专业学生,需要深究,建议参看专业教材深入理解其中玄妙
泰勒级数
完成对【泰勒公式】的理解后,需要对【级数 Series】这个概念进行一个推广,什么是【级数】呢?
在数学中,【级数】就是无限多项的和
在把泰勒展开式,扩展到无限项之后,就会出现【收敛 Converge】和【发散 diverge】的概念
收敛
收敛,即在泰勒展开式被推广到无限项之后,整体式子的值会越来越趋近于一个定值,比如下图的 $\frac{1}{2}$ 和 $e$
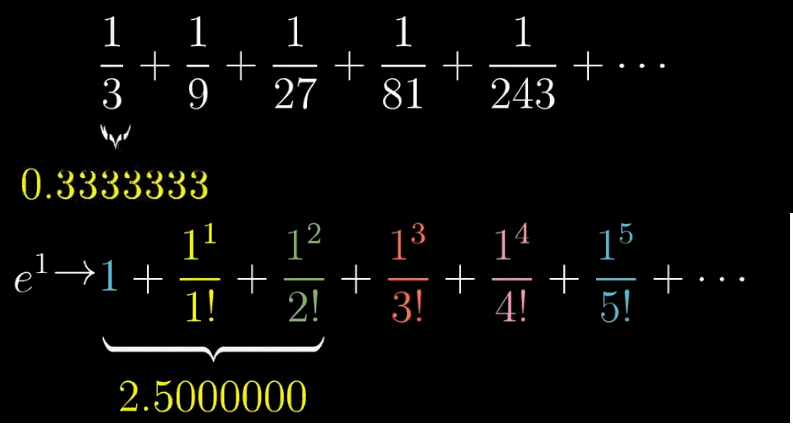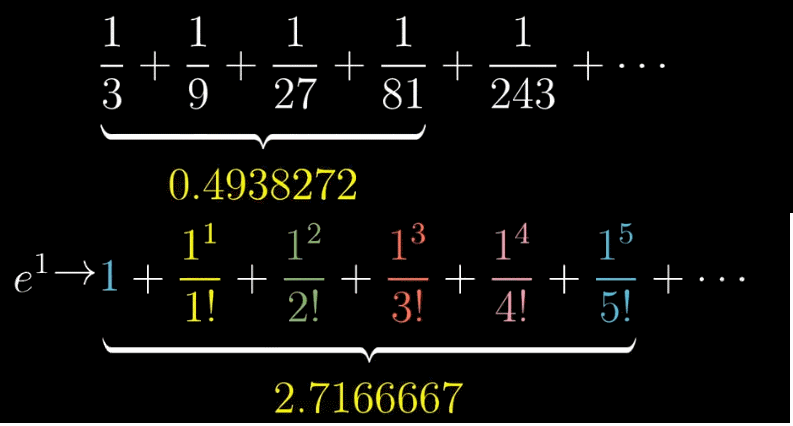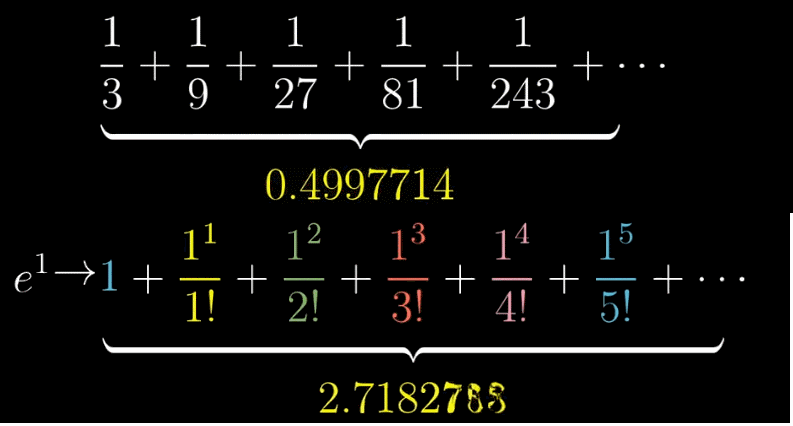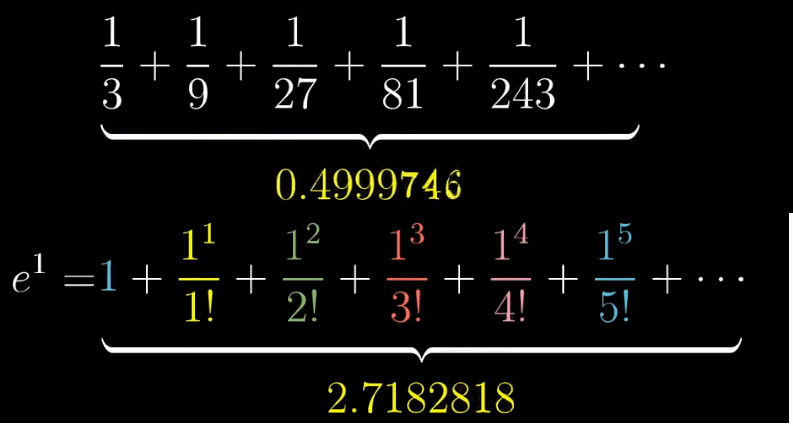
发散
与收敛相对应的,即发散,式子无法趋近于一个定值,比如 $ln(x)$ 在 $x=1$ 附近,如下图所示,虚线即为能够让多项式的和收敛的最大取之范围,称为【泰勒级数的收敛半径】
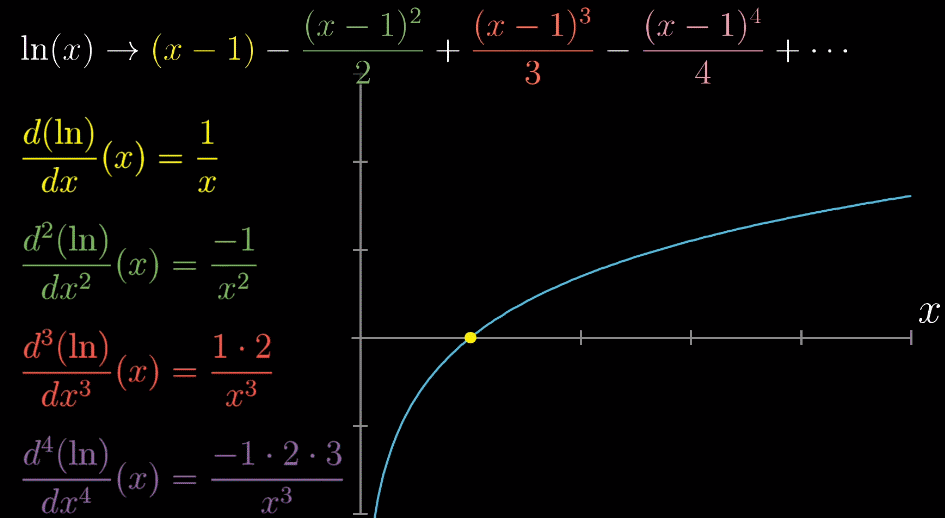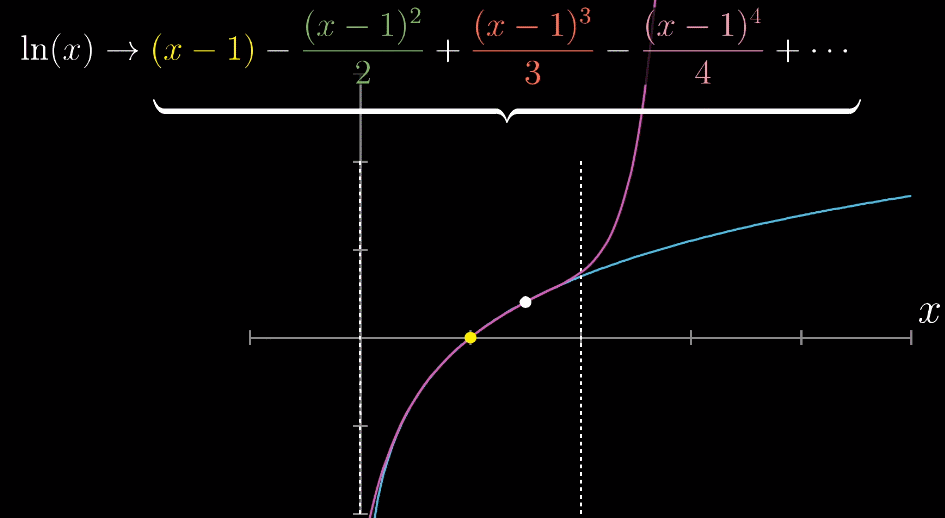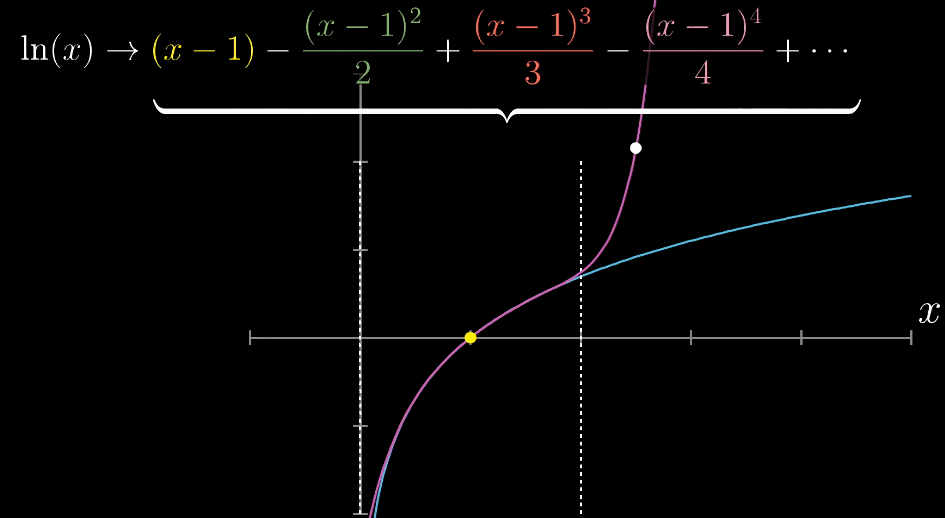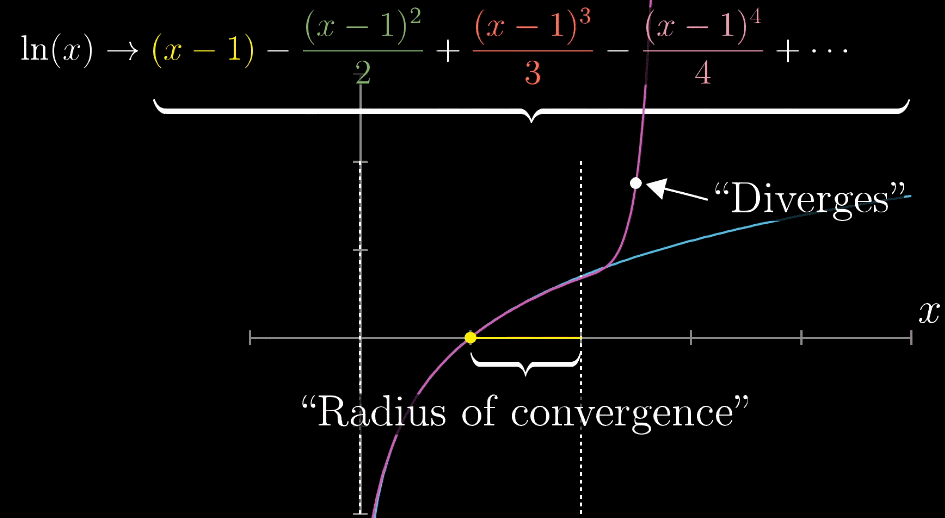
总结
- 泰勒公式干了一件什么事?
使用多项式表达式估计(近似) $f(x)$ 在 $x = a$ 附近的值
- 泰勒公式的导数项如何推倒出来的?
某一点处的导数值信息 $\iff$ 那一点附近的函数值信息
- 泰勒公式如何记永远不会忘?
参照第一条总结,是 $x=a$ 附近,公式 ➜ 多项式,很多项,要用求和写在一起;参照第二条总结,近似信息用的求导;系数就是对 $x=a$ 处求导一次一次放下来;OK,开始写!
$$ f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!} (x-a)^n $$并不知道写的对不对,翻到上面Check。OK,很完美,收工!





