【阅读时间】13min - 19min
【内容简介】详解解读什么是支持向量机,如何解支持向量以及涉及的拉普拉斯乘子法,还有核方法的解读
什么是支持向量机-SVM
支持向量机-SVM(Support Vector Machine)从本质来说是一种:用一条线(方程)分类两种事物
SVM的任务是找到这条分界线使得它到两边的margin都最大,注意,这里的横坐标是 $x_1$ 纵坐标为 $x_2$,如下图所示
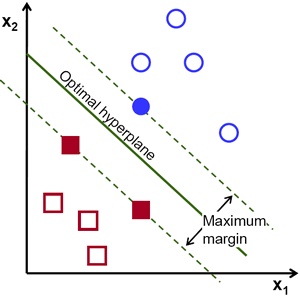
有了直观的感知,在定义这一节在做一些深入的思考,分解名词(Support Vector Machine)并尝试解释:
- Machine - Classification Machine 说明它的本质是一个分类器
- Support Vector - 如上图所示,在
Maximum Margin上的这些点就是支持向量,具体说即最终分类器表达式中只含有这些支持向量的信息,而与其他数据点无关。在下面的公式中,只有支持向量的系数 $\alpha_i$ 不等于0。说人话,上图中两个红色的点,一个蓝色的点,合起来就是支持向量 $$ \mathbf w \cdot \varphi (\mathbf x) = \sum_i \lambda_i y_i k(\mathbf x_i,\mathbf x) $$
公式中每一个符号的含义在后文有说明
如何求解支持向量机
对于我们需要求解的这个超平面(直线)来说,我们知道
- 它离两边一样远(待分类的两个部分的样本点)
- 最近的距离就是到支持向量中的点的距离
根据这两点,抽象SVM的直接表达(Directly Representation)
$$ arg \operatorname*{max}_{boundary} margin(boundary) \\ \text{所有正确归类的两类到boundary的距离} \ge margin \tag{1} $$注:$arg \operatorname*{max}_{x} f(x)$ 表示当 $f(x)$ 取最大值时,x的取值
其实这个公式是一点也不抽象,需要更进一步的用符号来表达。
我们知道在准确描述世界运行的规律这件事上,数学比文字要准确并且无歧义的多,文字(例子)直观啰嗦,数学(公式)准确简介
硬间隔
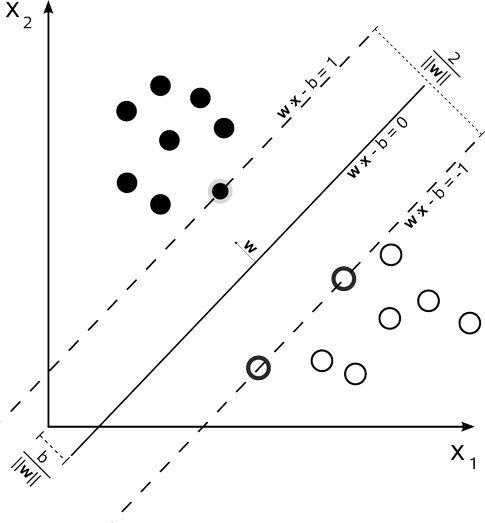
注:公式中加粗或者带有向量箭头的都表达一个向量
- 假设这些数据线性可分,也可称为硬间隔(Hard Margin)
- 首先定义超平面:$\mathbf w^T \vec x_i + b = 0$,接下来为了方便,设 $\vec x = (x_1,x_2)$ 即一条直线
- 任意点 $\vec x_i$ 到该直线的距离为 $\frac{1}{\lVert \mathbf w \lVert} (\mathbf w^T \vec x_i + b)$
- 对于空间内所有训练点的坐标记为 $(\vec x_i,y_i)$,其中 $y_i$ = 1 or -1, 表示点 $\vec x_i$ 所属的类
- 如果这些训练数据是线性可分的,选出两条直线(上图中的虚线),使得他们的距离尽可能的大,这两条直线的中央就是待求的超平面(直线)
为了表达直观,我们定义这两个超平面(直线)分别为 $\mathbf w^T \vec x_i + b = 1$ 和 $\mathbf w^T \vec x_i + b = -1$,两个超平面(直线)之间的距离为 $\gamma = \frac{2}{\lVert \mathbf w \lVert}$
注:选择
1的好处是,w和b进行尺缩变换(kw和kb)不改变距离,方便计算为了使得所有样本数据都在间隔区(两条虚线)以外,我们需要保证对于所有的 $i$ 满足下列的条件
- $\mathbf w^T \vec x_i + b \geqslant 1$ 若 $y_i = 1$
- $\mathbf w^T \vec x_i + b \leqslant -1$ 若 $y_i = -1$
- 上述两个条件可以写作 $y_i(\mathbf w^T \vec x_i + b) \geqslant 1, \;\text{for all 1}\; 1\leqslant i \leqslant n$ 这里的
n指样本点的数量 上面的表达(Directly Representation)可以被写成
$$ arg \operatorname*{max}_{\mathbf w,b} \left\{ {\frac{1}{\lVert \mathbf w \lVert} \operatorname*{min}_{n} [y_i(\mathbf w^T\vec x_i}+b)]\right\} \tag{2} $$最终目的是找到具有“最大间隔”(Maximum Margin)的划分超平面(直线),找到参数 $\mathbf w$ 和 $b$ 使得 $\gamma$ 最大
- 则可以对(2)式进行形式变换,得到 canonical representation $$ arg \operatorname*{max}_{\mathbf w,b} \frac{2}{\lVert \mathbf w \lVert} \implies arg \operatorname*{min}_{\mathbf w,b} \frac{1}{2}\lVert \mathbf w \lVert ^2 \\ s.t.\; y_i(\mathbf w^T\vec x_i+b) \geqslant1,\;i = 1,2,\ldots,m \tag{3} $$
注:
s.t.:subject to 表示约束条件,表达的意思等价于:为了使得所有样本数据都在间隔区(两条虚线)以外
为了解(3)式,需要用到拉格朗日乘子法(Method of lagrange multiplier),它是用来求解在约束条件目标函数的极值的,详细直观详解
注:以下解算过程希望完全看懂强烈建议理解阅读详细直观详解,很多地方推导过程只写必要过程及结论
根据约束的形式,我们引入m个拉格朗日乗法子,记为 $\boldsymbol \lambda = (\lambda_1,\ldots,\lambda_m)^T$ ,原因是,有m个约束,所以需要m个拉格朗日乗法子。可以得出拉格朗日方程如下:
$$
\mathcal{L}(\mathbf w,b,\boldsymbol \lambda) = \frac{1}{2}\lVert \mathbf w \lVert ^2 - \sum_{i=1}^m \lambda_i \{ y_i(\mathbf w^T\vec x_i+b) -1 \} \tag{4}
$$
解这个拉格朗日方程,对 $\mathbf w$ 和 $b$ 求偏导数,可以得到以下两个条件
$$
\mathbf w = \sum_{i=1}^m \lambda_i y_i \vec x_i \\
0 = \sum_{i=1}^m \lambda_i y_i
$$
将这两个条件带回公式(4),可以得到对偶形式(dual representaiton),我们的目的也变为最大化 $\mathcal{L}(\boldsymbol \lambda)$,表达式如下
$$
arg \operatorname*{max}_{\boldsymbol \lambda}\mathcal{L}(\boldsymbol \lambda) = \sum_{i=1}^m \lambda_i - \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \lambda_i \lambda_j \vec x_i \vec x_j \mathbf x_i^T \mathbf x_j \\
s.t. \qquad \lambda_i \geqslant 0, \forall i\;;\quad \sum_{i=1}^m \lambda_i y_i = 0 \tag{5}
$$
以上表达式可以通过二次规划算法解出 $\boldsymbol \lambda$ 后,带回,求出$\mathbf w$ 和 $b$,即可得到模型
$$
f(\mathbf x) = \mathbf w^T\mathbf x + b = \sum_{i=1}^m \lambda_i y_i \mathbf x_i^T \mathbf x + b \tag{6}
$$
补充一些关于二次规划算法的相关,(3)式的约束是一个不等式约束,所以我们可以使用KKT条件得到三个条件:
$$
\lambda_i \geqslant0 ;\quad y_i f(\mathbf x_i)-1 \geqslant0; \quad \lambda_i\{ y_i f(\mathbf x_i)-1 \}=0
$$
使用这些条件,可以构建高效算法来解这个方程,比如SMO(Sequential Minimal Optimization)就是其中一个比较著名的。至于SMO是如何做的,考虑到现代很多SVM的Pakage都是直接拿来用,秉承着前人付出了努力造了轮子就不重复造的核心精神,直接调用就好
软间隔
已经说明了如何求得方程,以上的推导形式都是建立在样本数据线性可分的基础上,如果样本数据你中有我我中有你(线性不可分),应该如何处理呢?这里就需要引入软间隔(Soft Margin),意味着,允许支持向量机在一定程度上出错

由上一节我们得知,约束为: $y_i(\mathbf w^T\vec x_i+b) \geqslant1,\;i = 1,2,\ldots,m$ ,目标是使目标函数可以在一定程度不满足这个约束条件,我们引入常数 $C$ 和 损失函数 $\ell_{0/1}(z)$ 为0/1损失函数,当z小于0函数值为1,否则函数值为0
$$
\operatorname*{min}_{\mathbf w,b} \frac{1}{2}\lVert w \lVert^2 + C \sum_{i=1}^m \ell_{0/1}(y_i(\mathbf w^T\vec x_i+b) -1) \tag {7}
$$
对于(7)式来说 $C \geqslant 0$ 是个常数,当C无穷大时,迫使所有样本均满足约束;当C取有限值时,允许一些样本不满足约束
但 $\ell_{0/1}(z)$ 损失函数非凸、非连续,数学性质不好,不易直接求解,我们用其他一些函数来代替它,叫做替代损失函数(surrogate loss)
$$
\begin{align}
& \text{hinge损失:} \ell_{hinge}(z) = max(0,1-z)\\
& \text{指数损失:} \ell_{exp}(z) = e^{-z}\\
& \text{对数损失:} \ell_{log}(z) = log(1+e^{-z})\\
\end{align}
$$
三种常见损失函数如下图

为了书写方便,我们引入松弛变量(slack variables): $\xi_i \geqslant 0$,可将(7)式重写为
$$
\operatorname*{min}_{\mathbf w,b,\xi_i} \frac{1}{2}\lVert w \lVert^2 + C \sum_{i=1}^m \xi_i \\ s.t. \quad y_i(\mathbf w^T\vec x_i+b) \geqslant 1 - \xi_i ;\; \xi_i \geqslant 0,\; i = 1,2,\ldots,m \tag{8}
$$
(8)式就是常见的软间隔支持向量机,其中,每一个样本都有一个对应的松弛变量,用以表征该样本不满足约束的程度,求解的方法同理硬间隔支持向量机
支持向量机扩展
核方法
以上我们求解的支持向量机都是在线性情况下的,那么非线性情况下如何处理?这里就引入:核方法
对于这样的问题,可以将样本从原始空间映射到一个更高为的特征空间,使得样本在这个特征空间内线性可分,直观可视化解释
为了完成这个目的,令 $\phi(\mathbf x)$ 表示将 $\mathbf x$ 映射后的特征向量,于是,在特征空间划分超平面所对应的模型可表示为:
$$
f(\mathbf x) = \mathbf w^T \phi(\mathbf x) + b
$$
同理上文中引入拉格朗日乘子,求解整个方程后可得
$$
\begin{align}
f(\mathbf x) &= \mathbf w^T \phi(\mathbf x) + b \\
&= \sum_{i=1}^m \lambda_i y_i \phi(\mathbf x_i)^T \phi(\mathbf x) + b \\
&= \sum_{i=1}^m \lambda_i y_i k(\mathbf x,\mathbf x_i)+ b
\end{align}
$$
这里的函数 $k(\cdot,\cdot)$ 就是核函数(kernel function),常见的核函数见下表
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核 | $\boldsymbol x_i^T \boldsymbol x_j$ | 无 |
| 多项式核 | $(\boldsymbol x_i^T \boldsymbol x_j)^d$ | $d \geqslant 1$ 多项式次数 |
| 高斯核 | $exp(-\frac{\lVert\boldsymbol x_i - \boldsymbol x_j \lVert^2}{2\sigma^2})$ | $\sigma>0$ 高斯核带宽 |
| 拉普拉斯核 | $exp(-\frac{\lVert\boldsymbol x_i - \boldsymbol x_j \lVert^2}{\sigma})$ | $\sigma>0$ |
| Sigmoid核 | $tanh(\beta \boldsymbol x_i^T\boldsymbol x_j + \theta)$ | $\beta>0$ $\theta>0$ |
也可以通过函数组合得到这些值
多类问题
多类问题可以使用两两做支持向量机,再由所有的支持向量机投票选出这个类别的归属,被称为one-versus-one approace。
