【阅读时间】21min - 24min 10999字
【内容简介】AlphaGo1.0详解链接,这篇AlphaGo Zero论文原文超详细翻译,并且总结了AlphaGo Zero的算法核心思路,附带收集了网上的相关评论
在之前的详解:深入浅出看懂AlphaGo中,详细定义的DeepMind团队定义围棋问题的结构,并且深入解读了AlphaGo1.0每下一步都发生了什么事,就在最近,AlphaGo Zero横空出世。个人观点是,如果你看了之前的文章,你就会觉得这是一个水到渠成的事情
另,如果你只对这个事件感兴趣的,而不想了解论文和技术细节,链接奉上,欢迎跳过到最后评论和总结部分(但这部分网上的大牛太多了,知乎答案内最高票对结合围棋的分析很漂亮!建议阅读)
上限置信区间算法(UCT),一种博弈树搜索算法,是AlphaGo中一个重要组成部分:MCTS搜索算法中的核心
法国南巴黎大学的数学家西尔万·热利(SylvainGelly)与巴黎技术学校的王毅早(YizaoWang,音译)将UCT集成到一个他们称之为MoGo的程序中。该程序的胜率竟然比先前最先进的蒙特卡罗扩展算法几乎高出了一倍。
2007年春季,MoGo在大棋盘比赛中也击败了实力稍弱的业余棋手,充分展示了能力。科奇什(UCT算法发明者)预言,10年以后,计算机就能攻克最后的壁垒,终结人类职业棋手对围棋的统治。今年是2017年,AlphaGo系列横空出世。10年,总有着天才的人具有先知般的远见。详见UTC算法
【小发现】看完论文发现,这篇文章的接受时间是2017年4月7号,审核完成时间是2017年9月13号,而在乌镇对阵柯洁(2017年5月23号)用的可能是AlphaGo Master(这里没法证据来证明到底是AlphaGo Zero还是AlphaGo Master)。这个团队也是无情啊,人类再一次感觉被耍了,根据Elo得分,Deepmind团队可能在赛前就透露过吧,即使是Master也有4858分啊,对于一个棋手来说,我感受到的是风萧萧兮易水寒决绝的背影。为柯洁的勇气打Call,当真围棋第一人,天下无双
论文正文内容详细解析
先上干货论文:Mastering the Game of Go without Human Knowledge ,之后会主要以翻译论文为主,在语言上尽量易懂,避免翻译腔
AlphaGo Zero,从本质上来说完全不同于打败樊麾和李世石的版本
- 算法上,自对弈强化学习,完全从随机落子开始,不用人类棋谱。之前使用了大量棋谱学习人类的下棋风格)
- 数据结构上,只有黑子白子两种状态。之前包含这个点的气等相关棋盘信息
- 模型上,使用一个神经网络。之前使用了策略网络(基于深度卷积神经网)学习人类的下棋风格,局面网络(基于左右互搏生成的棋谱,为什么这里需要使用左右互搏是因为现有的数据集不够,没法判断落子胜率这一更难的问题)来计算在当前局面下每一个不同落子的胜率
- 策略上,基于训练好的这个神经网,进行简单的树形搜索。之前会使用蒙特卡洛算法实时演算并且加权得出落子的位置
AlphaGo Zero 的强化学习
问题描述
在开始之前,必须再过一遍如何符号化的定义一个围棋问题
围棋问题,棋盘 19×19=361 个交叉点可供落子,每个点三种状态,白(用1表示),黑(用-1表示),无子(用0表示),用 $\vec s$ 描述此时棋盘的状态,即棋盘的状态向量记为 $ \vec s$ (state首字母)
$$
\vec s = (\underbrace{1,0,-1,\ldots}_{\text{361}})
$$
假设状态 $\vec s$ 下,暂不考虑不能落子的情况, 那么下一步可走的位置空间也是361个。将下一步的落子行动也用一个361维的向量来表示,记为 $\vec a$ (action首字母)
$$
\vec a = (0,\ldots,0,1,0,\ldots)
$$
公式1.2 假设其中1在向量中位置为39,则 $\vec a$ 表示在棋盘3行1列位置落白子,黑白交替进行
有以上定义,我们就把围棋问题转化为。
任意给定一个状态 $\vec s$ ,寻找最优的应对策略 $\vec a$ ,最终可以获得棋盘上的最大地盘
简而言之
看到 $\vec s$ ,脑海中就是一个棋盘,上面有很多黑白子
看到 $\vec a$ ,脑海中就想象一个人潇洒的落子
网络结构
新的网络中,使用了一个参数为 $\theta$ (需要通过训练来不断调整) 的深度神经网络$f_\theta$
- 【网络输入】
19×19×170/1值:现在棋盘状态的 $\vec s$ 以及7步历史落子记录。最后一个位置记录黑白,0白1黑,详见 - 【网络输出】两个输出:落子概率(
362个输出值)和一个评估值([-1,1]之间)记为 $f_{\theta}(\mathbf {\vec s}) = (\mathbf p,v)$- 【落子概率 $\mathbf p$】 向量表示下一步在每一个可能位置落子的概率,又称先验概率 (加上不下的选择),即 $p_a = Pr(\vec a|\mathbf {\vec s})$ (公式表示在当前输入条件下在每个可能点落子的概率)
- 【评估值 $v$】 表示现在准备下当前这步棋的选手在输入的这八步历史局面 $\vec s$ 下的胜率(我这里强调局面是因为网络的输入其实包含历史对战过程)
- 【网络结构】基于Residual Network(大名鼎鼎ImageNet冠军ResNet)的卷积网络,包含20或40个Residual Block(残差模块),加入批量归一化Batch normalisation与非线性整流器rectifier non-linearities模块
改进的强化学习算法
自对弈强化学习算法(什么是强化学习,非常建议先看看强化学习的一些基本思想和步骤,有利于理解下面策略、价值的概念,推荐系列笔记)
在每一个状态 $\vec s$ ,利用深度神经网络 $f_\theta$ 预测作为参照执行MCTS搜索(蒙特卡洛搜索树算法),MCTS搜索的输出是每一个状态下在不同位置对应的概率 $\boldsymbol \pi$ (注意这里是一个向量,里面的值是MCTS搜索得出的概率值),一种策略,从人类的眼光来看,就是看到现在局面,选择下在每个不同的落子的点的概率。如下面公式的例子,下在$(1,3)$位置的概率是0.92,有很高概率选这个点作为落子点
$$
\boldsymbol \pi_i = (\underbrace{0.01,0.02,0.92,\ldots}_{\text{361}})
$$
MCTS搜索得出的落子概率比 $f_\theta$ 输出的仅使用神经网络输出的落子概率 $\mathbf p$ 更强,因此,MCTS可以被视为一个强力的策略改善(policy improvement)过程
使用基于MCTS提升后的策略(policy)来进行落子,然后用自对弈最终对局的胜者 $z$ 作为价值(Value),作为一个强力的策略评估(policy evaluation)过程
并用上述的规则,完成一个通用策略迭代算法去更新神经网络的参数 $\theta$ ,使得神经网络输出的落子概率和评估值,即 $f_{\theta}(\mathbf {\vec s}) = (\mathbf p,v)$ 更加贴近能把这盘棋局赢下的落子方式(使用不断提升的MCST搜索落子策略$\boldsymbol \pi$ 和自对弈的胜者 $z$ 作为调整依据)。并且,在下轮迭代中使用新的参数来进行自对弈
在这里补充强化学习的通用策略迭代(Generalized Policy Iteration)方法
从策略 $\pi_0$ 开始
策略评估(Policy Evaluation)- 得到策略 $\pi_0$ 的价值 $v_{\pi_0}$ (对于围棋问题,即这一步棋是好棋还是臭棋)
策略改善(Policy Improvement)- 根据价值 $v_{\pi_0}$,优化策略为 $\pi_{0+1}$ (即人类学习的过程,加强对棋局的判断能力,做出更好的判断)
迭代上面的步骤2和3,直到找到最优价值 $v_*$ ,可以得到最优策略 $\pi_*$
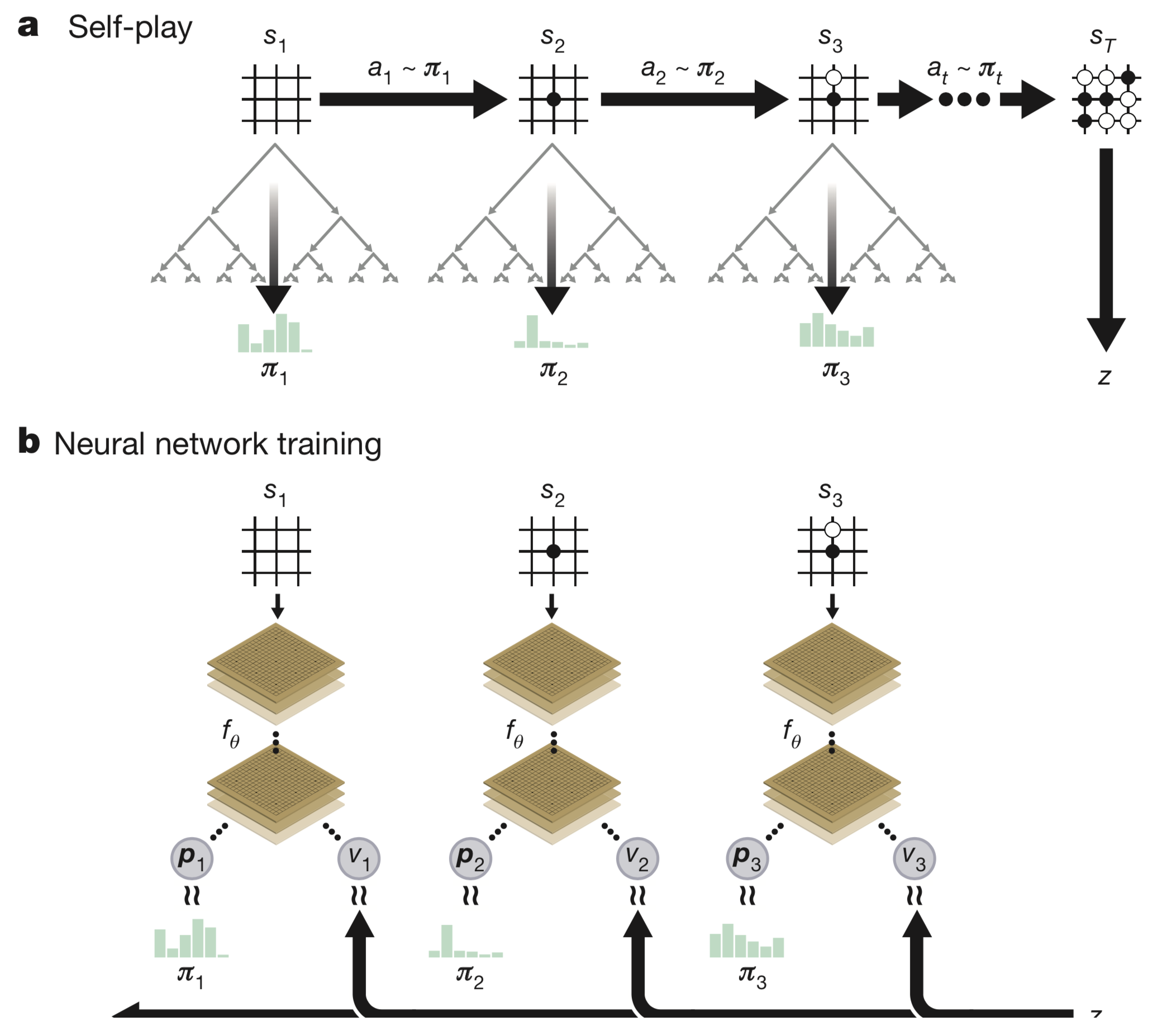
【a图】表示自对弈过程 $s_1,\ldots,s_T$。在每一个位置 $s_t$ ,使用最新的神经网络 $f_\theta$ 执行一次MCTS搜索 $\alpha_\theta$ 。根据搜索得出的概率 $a_t \sim \boldsymbol \pi_i$ 进行落子。终局 $s_T$ 时根据围棋规则计算胜者 $z$
$\pi_i$ 是每一步时执行MCTS搜索得出的结果(柱状图表示概率的高低)
【b图】表示更新神经网络参数过程。使用原始落子状态 $\vec s_t$ 作为输入,得到此棋盘状态 $\vec s_t$ 下下一步所有可能落子位置的概率分布 $\mathbf p_t$ 和当前状态 $\vec s_t$ 下选手的赢棋评估值 $v_t$
以最大化 $\mathbf p_t$ 与 $\pi_t$ 相似度和最小化预测的胜者 $v_t$ 和局终胜者 $z$ 的误差来更新神经网络参数 $\theta$ (详见公式1) ,更新参数 $\theta$ ,下一轮迭代中使用新神经网络进行自我对弈
我们知道,最初的蒙特卡洛树搜索算法是使用随机来进行模拟,在AlphaGo1.0中使用局面函数辅助策略函数作为落子的参考进行模拟。在最新的模型中,蒙特卡洛搜索树使用神经网络 $f_\theta$ 的输出来作为落子的参考(详见下图Figure 2)
每一条边 $(\vec s,\vec a)$ (每个状态下的落子选择)保存的是三个值:先验概率 $P(\vec s,\vec a)$,访问次数 $N(\vec s,\vec a)$,行动价值 $Q(\vec s,\vec a)$。
每次模拟(模拟一盘棋,直到分出胜负)从根状态开始,每次落子最大化上限置信区间 $Q(\vec s,\vec a) + U(\vec s,\vec a)$ 其中 $U(\vec s,\vec a) \propto \frac{P(\vec s,\vec a)}{1 + N(\vec s,\vec a)}$ 直到遇到叶子节点 $s’$
叶子节点(终局)只会被产生一次用于产生先验概率和评估值,符号表示即 $f_\theta(s’) = (P(s’,\cdot), V(s’))$
模拟过程中遍历每条边 $(\vec s, \vec a)$ 时更新记录的统计数据。访问次数加一 $N(\vec s,\vec a) += 1$;更新行动价值为整个模拟过程的平均值,即 $Q(\vec s, \vec a) = \frac {1}{N(\vec s, \vec a)}\Sigma_{\vec s'|\vec s, \vec a \Rightarrow \vec s'}V(\vec s')$ ,$\vec s’|\vec s, \vec a \Rightarrow \vec s’$ 表示在模拟过程中从 $\vec s$ 走到 $\vec s’$的所有落子行动 $\vec a$
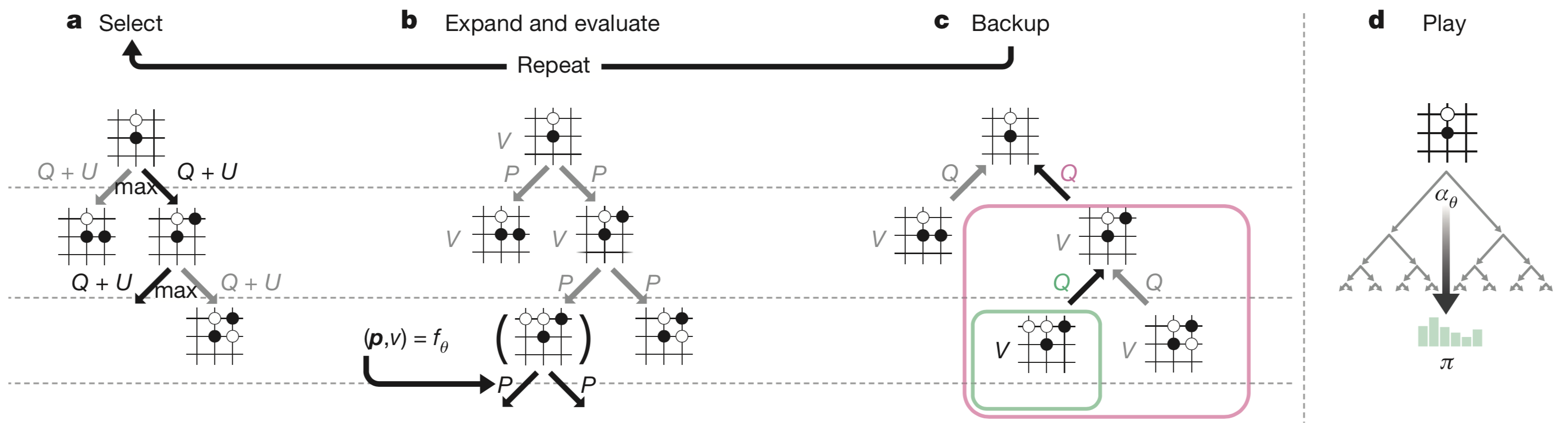
【a图】表示模拟过程中遍历时选 $Q+U$ 更大的作为落子点
【b图】叶子节点 $s_L$ 的扩展和评估。使用神经网络对状态 $s_L$ 进行评估,即 $f_\theta(s_L) = (P(s_L,\cdot), V(s_L))$ ,其中 $\mathbf P$ 的值存储在叶子节点扩展的边中
【c图】更新行动价值 $Q$ 等于此时根状态 $\vec s$ 所有子树评估值 $V$ 的平均值
【d图】当MCTS搜索完成后,返回这个状态 $\vec s$ 下每一个位置的落子概率 $\boldsymbol \pi$,成比例于 $N^{1/\tau}$($N$为访问次数,$\tau$ 为控温常数)
更加具体的详解见:搜索算法
MCTS搜索可以看成一个自对弈过程中决定每一步如何下的依据,根据神经网络的参数 $\theta$ 和根的状态 $\vec s$ 去计算每个状态下落子位置的先验概率,记为 $\boldsymbol \pi = \alpha_\theta(\vec s)$ ,幂指数正比于访问次数 $\pi_{\vec a} \propto N(\vec s, \vec a)^{1/\tau}$,$\tau$ 是温度常数
训练步骤总结
使用MCTS下每一步棋,进行自对弈,强化学习算法(必须了解通用策略迭代的基本方法)的迭代过程中训练神经网络
- 神经网络参数随机初始化 $\theta_0$
- 每一轮迭代 $i \geqslant 1$ ,都自对弈一盘(见Figure-1a)
- 第 $t$ 步:MCTS搜索 $\boldsymbol \pi_t = \alpha_{\theta_{i-1}}(s_t)$ 使用前一次迭代的神经网络 $f_{\theta_{i-1}}$,根据MCTS结构计算出的落子策略 $\boldsymbol \pi_t$ 的联合分布进行【采样】再落子
- 在 $T$ 步 :双方都选择跳过;搜索时评估值低于投降线;棋盘无地落子。根据胜负得到奖励值Reward $r_T \in \{-1,+1\}$。
- MCTS搜索下至中盘的过程的每一个第 $t$ 步的数据存储为 $\vec s_t,\mathbf \pi_t, z_t$ ,其中 $z_t = \pm r_T$ 表示在第 $t$ 步时的胜者
- 同时,从上一步 $\vec s$ 迭代时自对弈棋局过程中产生的数据 $(\vec s, \boldsymbol \pi, z)$ ($\vec s$ 为训练数据,$\boldsymbol \pi, z$ 为标签)中采样(这里的采样是指选Mini-Batch)来训练网络参数 $\theta_i$,
- 神经网络 $f_{\theta_i}(\vec s) = (\mathbf p, v)$以最大化 $\mathbf p_t$ 与 $\pi_t$ 相似度和最小化预测的胜者 $v_t$ 和局终胜者 $z$ 的误差来更新神经网络参数 $\theta$ ,损失函数公式如下
其中 $c$ 是
L2正则化的系数
AlphaGo Zero训练过程中的经验
最开始,使用完全的随机落子训练持续了大概3天。训练过程中,产生490万场自对弈,每次MCTS大约1600次模拟,每一步使用的时间0.4秒。使用了2048个位置的70万个Mini-Batches来进行训练。
训练结果如下,图3
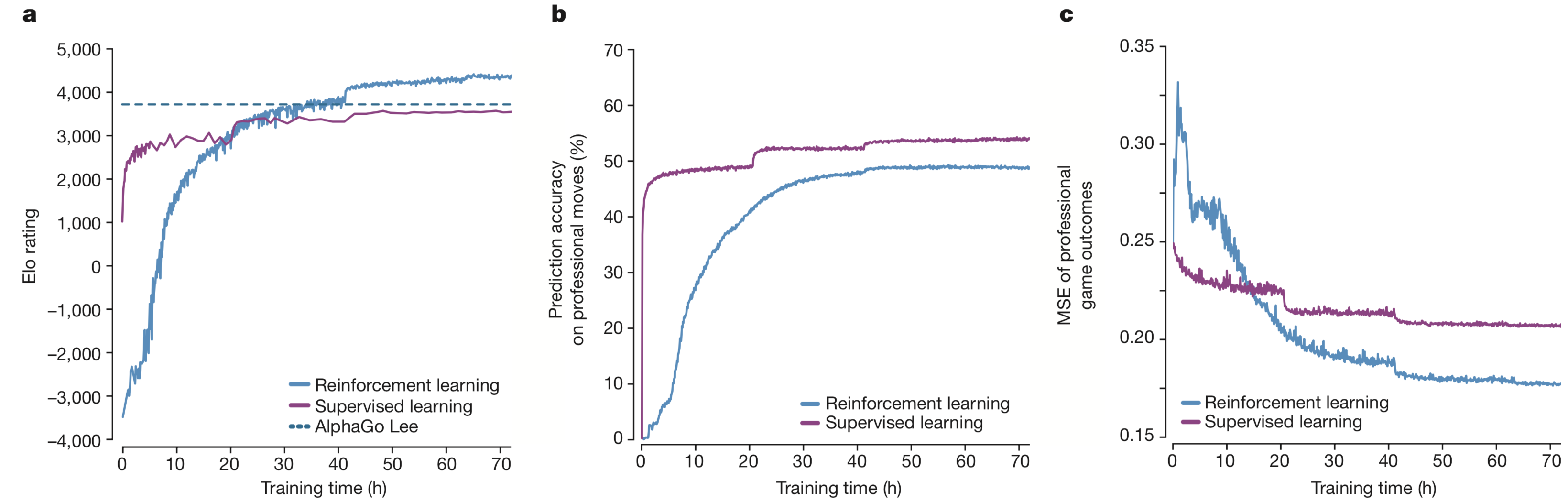
【a图】表示随时间AlphaGo Zero棋力的增长情况,显示了每一个不同的棋手 $\alpha_{\theta_i}$ 在每一次强化学习迭代时的表现,可以看到,它的增长曲线非常平滑,没有很明显的震荡,稳定性很好
【b图】表示的是预测准确率基于不同迭代第$i$轮的 $f_{\theta_i}$
【c图】表示的MSE(平方误差)
在24小时的学习后,无人工因素的强化学习方案就打败了通过模仿人类棋谱的监督学习方法
为了分别评估结构和算法对结构的影响,得到了,下图4
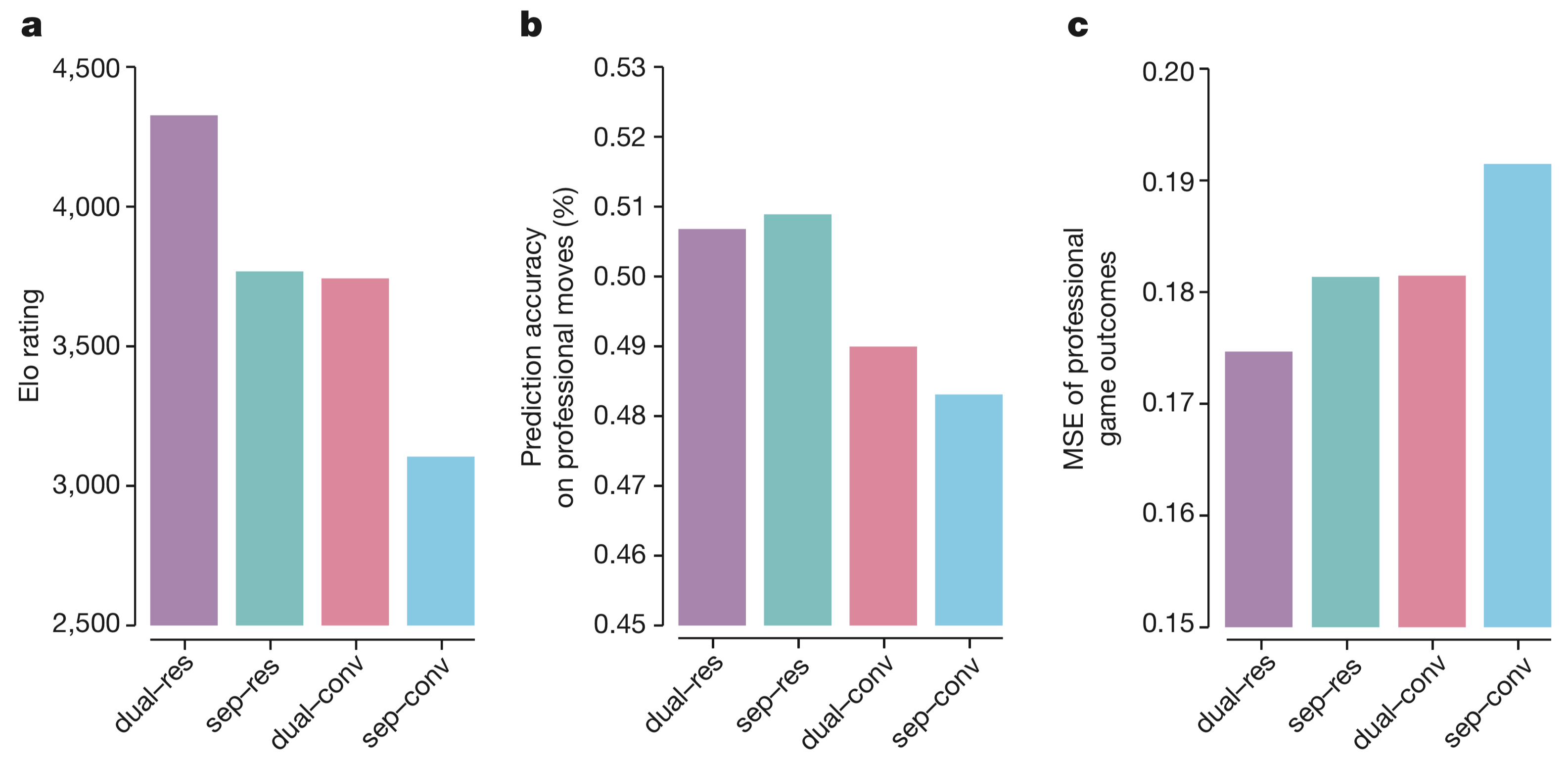
【dual-res】表示 AlphaGo Zero(20个模块),策略头和评估值头由一个网络产生
【sep-res】表示使用20个残差模块,策略头和评估值头被分成两个不同的网络
【dual-conv】表示不用ResNet,使用12层卷积网,同时包括策略头和评估值头
【sep-conv】表示 AlphaGo Lee(击败李世乭的)使用的网络结构,策略头和评估值头被分成两个不同的网络
AlphaGo Zero学到的知识
在训练过程中,AlphaGo Zero可以一步步的学习到一些特殊的围棋技巧(定式),如图5
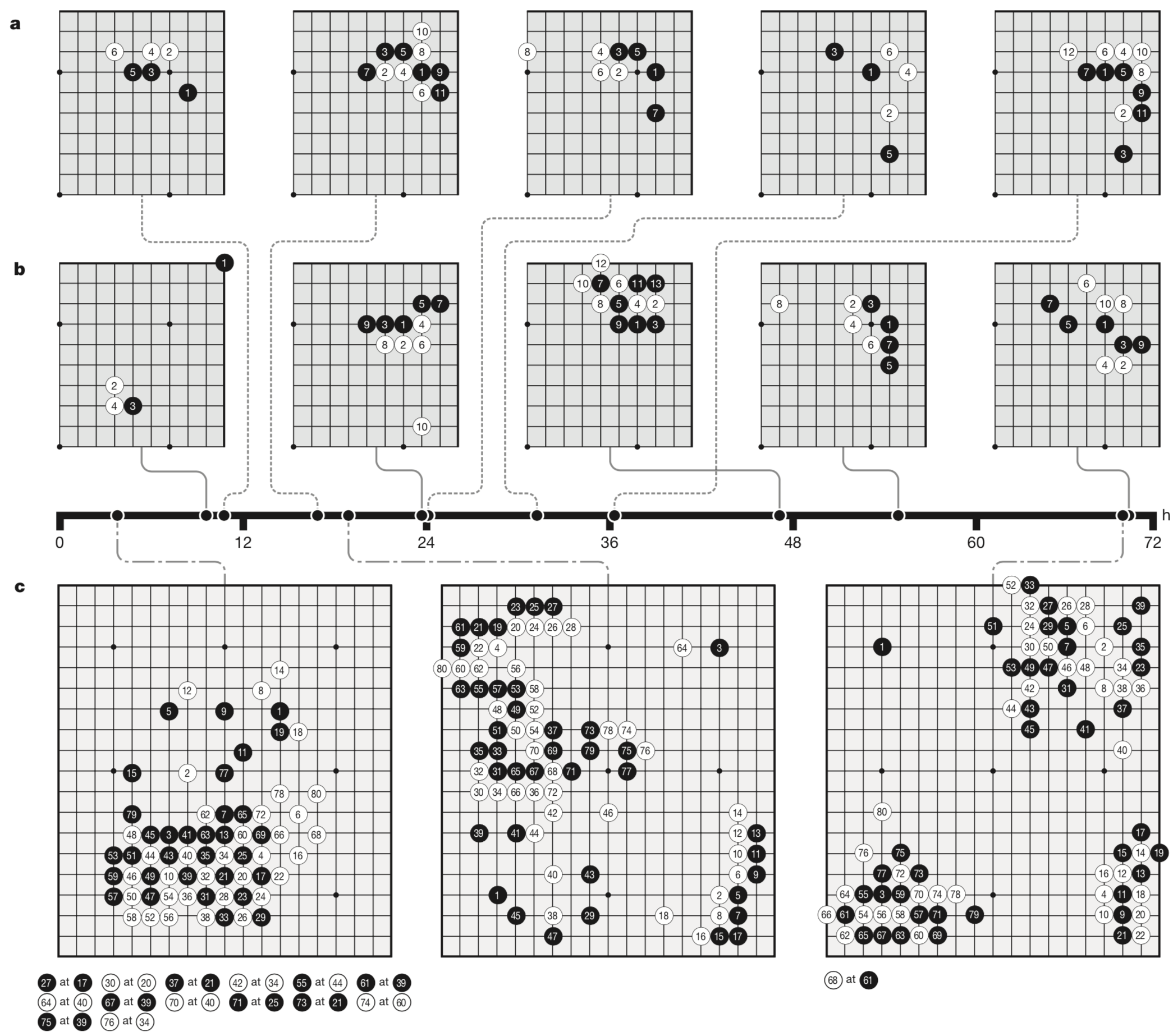
中间的黑色横轴表示的是学习时间
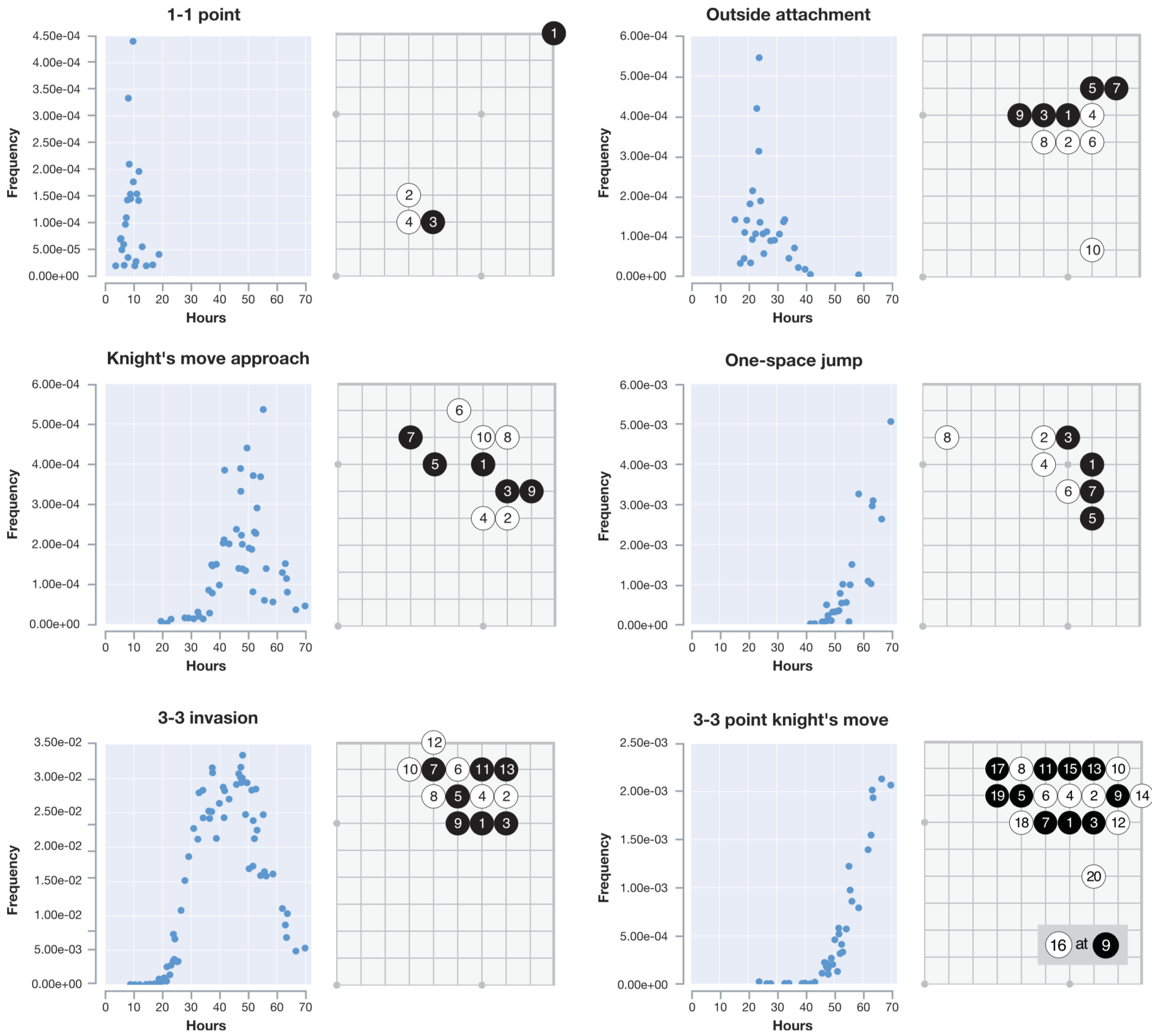
【a图】对应的5张棋谱展现的是不同阶段AlphaGo Zero在自对弈过过程中展现出来的围棋定式上的新发现
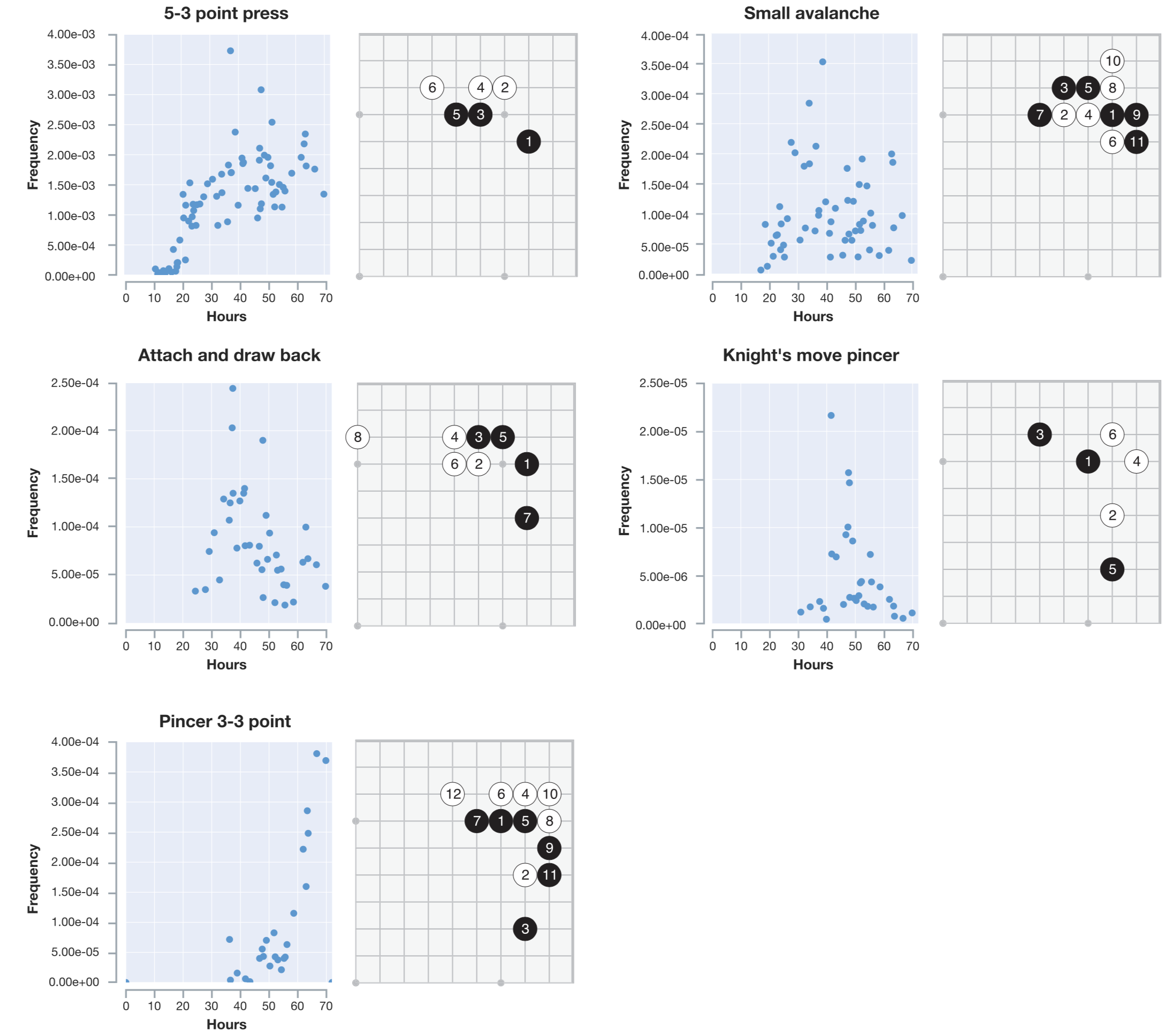
【b图】展示在右星位上的定式下法的进化。可以看到训练到50小时,点三三出现了,但再往后训练,b图中的第五种定式高频率出现,在AlphGa Zero看来,这一种形式似乎更加强大
【c图】展现了前80手自对弈的棋谱伴随时间,明显有很大的提升,在第三幅图中,已经展现出了比较明显的围的倾向性
具体频率图见:出现频率随训练时间分布图
AlphaGo Zero的最终实力
之后,最终的AlphaGo Zero 使用40个残差模块,训练接近40天。在训练过程中,产生了2900万盘的自对弈棋谱,使用了310万个Mini-Batches来训练神经网络,每一个Mini-Batch包含了2048个不同的状态。(覆盖的状态数是63亿($10^{10}$),但和围棋的解空间 $2^{361} \approx 10^{108}$ 相比真的很小,也从侧面反映出,围棋中大部分选择都是冗余的。在一个棋盘局面下,根据先验概率,估计只有15-20种下法是值得考虑的)
被评测不同版本使用计算力的情况,AlphaGo Zero和AlphaGo Master被部署到有4个TPUs的单机上运行(主要用于做模型的输出预测Inference和MCTS搜索),AlphaGo Fan(打败樊麾版本)和AlphaGo Lee(打败李世乭版本) 分布式部署到机器群里,总计有176GPUs和48GPUs(Goolge真有钱)。还加入了raw network,它是每一步的仅仅使用训练好的深度学习神经网的输出 $\mathbf p_a$ 为依据选择最大概率点来落子,不使用MCTS搜索(Raw Network裸用深度神经网络的输出已经十分强大,甚至已经接近了AlphaGo Fan)
下图6展示不同种AlphaGo版本的棋力情况
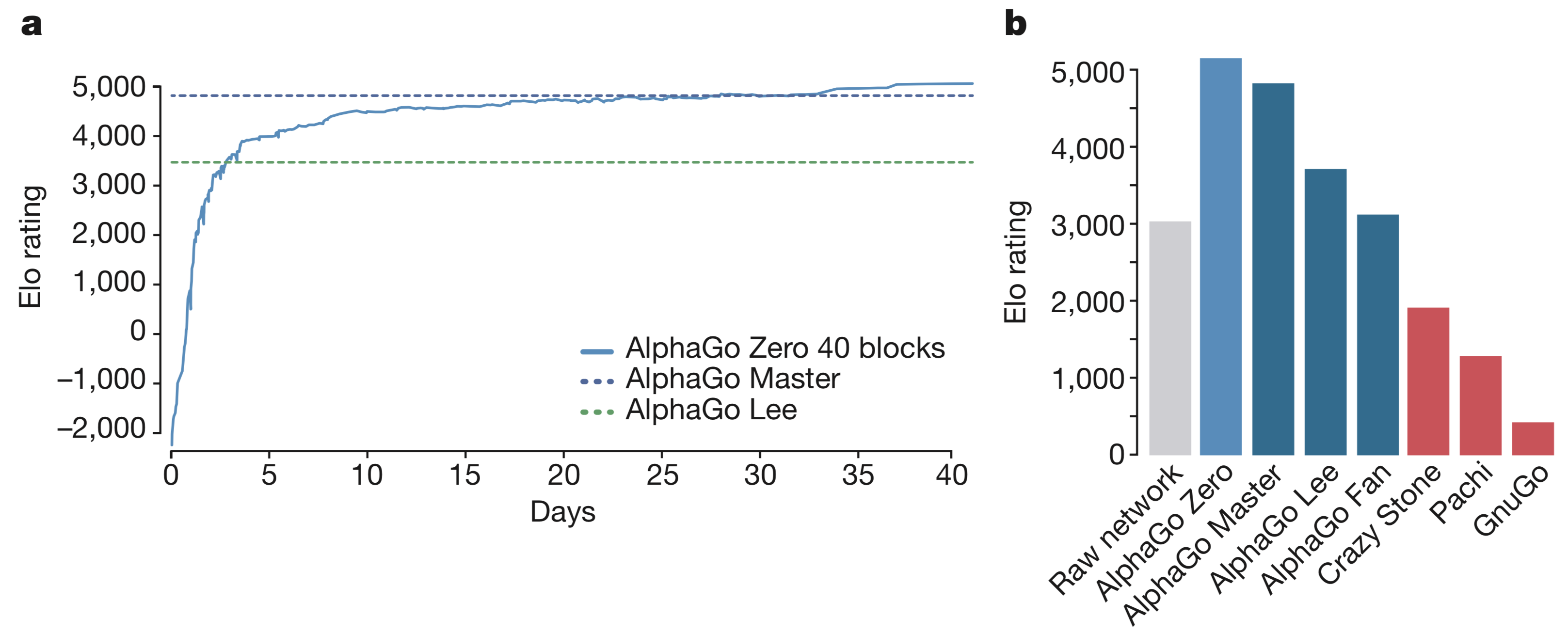
【a图】随着训练时间棋力的增强曲线
【b图】裸神经网络得分3055,AlphaGo Zero得分5185,AlphaGo Master得分4858,AlphaGo Lee得分3738,AlphaGo Fan得分3144
最终,AlphaGo Zero 与 AlphaGo Master的对战比分为89:11,对局中限制一场比赛在2小时之内(新闻中的零封是对下赢李世乭的AlphaGo Lee)
论文附录内容
我们知道,Nature上的文章一般都是很强的可读性和严谨性,每一篇文章的正文可能只有4-5页,但是附录一般会远长于正文。基本所有你的技术细节疑惑都可以在其中找到结果,这里值列举一些我自己比较感兴趣的点,如果你是专业人士,甚至想复现AlphaGo Zero,读原文更好更精确
围棋领域先验知识
AlphaGo Zero最主要的贡献是证明了没有人类的先验知识机器也可以在性能上超越人类。为了阐释清楚这种贡献来自于何处,我们列举一些AlphaGo Zero使用到的知识,无论是训练过工程中的还是MCTS搜索中的。如果你想把AlphaGo Zero的思路应用的到解决其他游戏问题上,这些内容可能需要被替换
围棋基本规则
无论实在MCTS搜索中的模拟还是自对弈的过程,都依赖游戏最终的胜负规则,并且在落子过程中,根据规则还可以排除一部分不可以落子的点(比如已经落子的点,无法确认在AlphaGo Zero还有气为零的点不能下这个规则,因为不记录气的信息了。但可以写一个函数来判断当前局面 $\vec s$ 下下一步所有可能的落子点,不一定非得计算这个信息,这个过程可以完全多线程)
Tromp-Taylor规则
在AlphaGo Zero中使用的是PSK(Positional Superko)禁全同规则(中国,韩国及日本使用),只要这一手(不包括跳过)会导致再现之前的局面,就禁止。
旋转与镜面
对于围棋来说,几个状态 $\vec s$ 在经过旋转或反射后是完全相同的,这种规律可以用来优化训练数据和MCTS搜索中的子树替换策略。并且因为贴目(黑棋先下优势贴目7目半)规则存在,不同状态 $\vec s$ 换颜色也是相同的。这个规则可以用来使用当前下子的棋手的角度来表示棋盘
除了以上的三个规则,AlphaGo Zero 没有使用其他任何先验知识,它仅仅使用深度神经网络对叶子节点进行评估并选择落子位置。它没有使用任何Rollout Policy(这里指的应该是AlphaGo之前版本的快速走子策略)或者树形规则,MCTS搜索也没有使用其他的标准启发式规则或者先验常识规则去进行增强
整个算法从随机初始化神经网络参数开始。网络结构和超参数选择 见下一节。MCTS搜索的超参数 $c_{puct}$ 由高斯过程优化决定,为了优化自对弈的性能,使用了一个神经网络进行预训练。对于一个大规模网络的训练过程(40个残差模块,40天),使用一个小规模网络(20个残差模块,3天)来反复优化MCTS搜索的超参数 $c_{puct}$。整个训练过程没有任何人工干预
自对弈训练工作流
AlphaGo Zero的工作流由三个模块构成,可以异步多线程进行:
- 深度神经网络参数 $\theta_i$ 根据自对弈数据持续优化
- 持续对棋手 $\alpha_{\theta_i}$ 棋力值进行评估
- 使用表现最好的 $\alpha_{\theta_*}$ 用来产生新的自对弈数据
优化参数
每一个神经网络 $f_{\theta_i}$ 在64个GPU工作节点和19个CPU参数服务器上进行优化。
每个工作节点的批次(Batch)大小是32,每一个mini-batch大小为2048。每一个 mini-batch 的数据从最近50万盘的自对弈棋谱的状态中联合随机采样。
神经网络权重更新使用带有动量(momentum)和学习率退火(learning rate annealing)的随机梯度下降法(SGD),损失函数见公式1
学习率退火比率见下表
| 步数(千) | 强化学习率 | 监督学习率 |
|---|---|---|
| 0-200 | $10^{-2}$ | $10^{-1}$ |
| 200-400 | $10^{-2}$ | $10^{-2}$ |
| 400-600 | $10^{-3}$ | $10^{-3}$ |
| 600-700 | $10^{-4}$ | $10^{-4}$ |
| 700-800 | $10^{-4}$ | $10^{-5}$ |
| >800 | $10^{-4}$ | - |
动量参数设置为0.9
方差项和交叉项的权重相同,原因是奖励值被归一化到 $r \in [-1,+1]$
L2正则化系数设置为 $c = 10^{-4}$
优化过程每1000个训练步数执行一次,并使用这个新模型来生成下一个Batch的自对弈棋谱
评估器
为了保证生成数据的质量(不至于棋力反而下降),在使用新的神经网络去生成自对弈棋谱前,用现有的最好网络 $f_{\theta_*}$ 来对它进行评估
【评估神经网络 $f_{\theta_i}$ 的方法】使用 $f_{\theta_i}$ 进行MCTS搜索得出的 $\alpha_{\theta_i}$ 的性能(得到 $\alpha_{\theta_i}$ 的MCTS搜索过程中使用 $f_{\theta_i}$ 去估计叶子节点的位置和先验概率,详见MCTS搜索这一节)
每一个评估由400盘对局组成,MCTS搜索使用1600次模拟,将温度参数设为无穷小 $\tau \Rightarrow 0$(目的是为了使用最多访问次数的落子下法去下,追求最强的棋力),如果新的选手 $\alpha_{\theta_i}$ 在这400盘中胜率大于55%,将这个选手更新为最佳选手 $\alpha_{\theta_*}$ ,用来产生下一轮的自对弈棋谱,并且设为下一轮的比较对象
自对弈
通过评估器,现在已经有一个当前的最好棋手 $\alpha_{\theta_*}$,使用它来产生数据。每次迭代中, $\alpha_{\theta_*}$ 自对弈25000盘,其中每一步MCTS搜索模拟1600次(模拟的每次落子大约0.4秒,这里的一次表示的就是MCTS搜索中走到叶子节点,得出胜负结果)
前30步,温度 $\tau = 1$,与MCTS搜索中的访问次数成正比,目的是保证前30步下法的多样性。在之后的棋局中,温度设为无穷小。并在先验概率中加入狄利克雷噪声 $P(\vec s, \vec a) = (1 - \epsilon) p_{\vec a} + \epsilon \eta_{\vec a}$ ,其中 $\eta \sim Dir(0.03)$ 且 $\epsilon = 0.25$。这个噪声保证所有的落子可能都会被尝试,但也可能下出臭棋
投降阈值 $v_{rerign}$ 自动设为错误正类率(如果AlphaGo没有投降可以赢的比例)小于5%,为了测量错误正类(false positives),在10%的自对弈中关闭投降机制,必须下完
监督学习
为了进行对比,我们还使用监督学习训练了一个参数为 $\theta_{SL}$ 神经网络。神经网络的结构和AlphaGo Zero相同。数据集 $(\vec s, \boldsymbol \pi, z)$ 随机采样自KGS数据集,人类的落子策略位置即设置 $\pi_a = 1$ 。使用同样的超参数和损失函数,但是平方误差的系数为0.01,学习率图参照上表的第二列。其他超参数和上一节相同
比AlphaGo1.0z中使用两种网络,使用这种结构的网络,可以有效的防止过拟合。并且实验也证明这个网络结构的的效果要好于之前的网络
MCTS搜索算法
这一部分详解的AlphaGo Zero的算法核心示意图Figure2
AlphaGo Zero使用的是比AlphaGo1.0中更简单的异步策略价值MCTS搜索算法(APV-MCTS)的变种
搜索树中的节点 $\vec s$ 包含一条边 $(\vec s,\vec a)$ 对应所有可能的落子 $\vec a \in \mathcal A(\vec s)$ ,每一条边中存储一个数据,包含下列公式的四个值
$$
{N(\vec s,\vec a), W(\vec s,\vec a), Q(\vec s,\vec a), P(\vec s,\vec a)}
$$
$N(\vec s,\vec a)$ 表示MCST搜索模拟走到叶子节点的过程中的访问次数
$W(\vec s,\vec a)$ 表示行动价值(由路径上所有的 $v$ 组成)的总和
$Q(\vec s,\vec a)$ 表示行动价值的均值
$P(\vec s,\vec a)$ 表示选择这条边的先验概率(一个单独的值)
多线程(并行)执行多次模拟,每一次迭代过程先重复执行1600次Figure 2中的前3个步骤,计算出一个 $\boldsymbol \pi$ ,根据这个向量下现在的这一步棋
Selcet - Figure2a
MCTS中的选择步骤和之前的版本相似,详见AlphaGo之前的详解文章,这篇博文详细通俗的解读了这个过程。概括来说,假设L步走到叶子节点,当走第 $t < L$ 步时,根据搜索树的统计概率落子
$$
\vec a_t = \operatorname*{argmax}_{\vec a}(Q(\vec s_t, \vec a) + U (\vec s_t, \vec a))
$$
其中计算 $U (\vec s_t, \vec a)$ 使用PUCT算法的变体
$$ U(\vec s, \vec a) = c_{puct}P(\vec s, \vec a) \frac{\sqrt{\Sigma_{\vec b} N(\vec s, \vec b)}}{1 + N(\vec s, \vec a)} $$其中 $c_{puct}$ 是一个常数。这种搜索策略落子选择最开始更趋向于高先验概率和低访问次数的,但逐渐的会更加趋向于选择有着更高行动价值的落子
$c_{puct}$ 使用贝叶斯高斯过程优化来确定
Expand and evaluate - Figure 2b
将叶子节点 $\vec s_L$ 加到队列中等待输入至神经网络进行评估, $f_\theta(d_i(\vec s_L)) = (d_i(p), v)$ ,其中 $d_i$ 表示一个1至8的随机数来表示双方向镜面和旋转(从8个不同的方向进行评估,如下图所示,围棋棋型在很多情况如果从视觉角度来提取特征来说是同一个节点,极大的缩小了搜索空间)
队列中8个不同位置组成一个大小为8的mini-batch输入到神经网络中进行评估。整个MCTS搜索线程被锁死直到评估过程完成(这个锁死是保证并行运算间同步)。叶子节点被展开(Expand),每一条边 $(\vec s_L,\vec a)$被初始化为
$$ {N(\vec s_L,\vec a) = 0 ;\; W(\vec s_L,\vec a) = 0; \; Q(\vec s_L,\vec a) = 0\\P(\vec s_L,\vec a) = p_a} $$这里的 $p_a$ 由将 $\vec s$ 输入神经网络得出 $\mathbf p$ (包括所有落子可能的概率值 $p_a$),然后将神经网络的输出值 $v$ 传回(backed up)
Backup - Figure 2c
沿着扩展到叶子节点的路线回溯将边的统计数据更新(如下列公式所示)
$$ N(\vec s_t, \vec a_t) = N(\vec s_t, \vec a_t) + 1 \\ W(\vec s_t, \vec a_t) = W(\vec s_t, \vec a_t) + v \\ Q(\vec s_t, \vec a_t) = \frac{W(\vec s_t, \vec a_t) }{N(\vec s_t, \vec a_t) } $$注解:在 $W(\vec s_t, \vec a_t)$ 的更新中,使用了神经网络的输出 $v$,而最后的价值就是策略评估中的这一状态的价值 $Q(\vec s, \vec a)$
使用虚拟损失(virtual loss)确保每一个线程评估不同的节点。实现方法概括为把其他节点减去一个很大的值,避免其他搜索进程走相同的路,详见
Play - Figure 2d
完成MCTS搜索(并行重复1-3步1600次,花费0.4s)后,AlphaGo Zero才从 $\vec s_0$ 状态下走出第一步 $\vec a_0$,与访问次数成幂指数比例
$$ \boldsymbol \pi(\vec a|\vec s_0) = \frac {N(\vec s_0,a)^{1/\tau}}{\Sigma_{\vec b} N(\vec s_0, \vec b)^{1/\tau}} $$其中 $\tau$ 是一个温度常数用来控制探索等级(level of exploration)。它是热力学玻尔兹曼分布的一种变形。温度较高的时候,分布更加均匀(走子多样性强);温度降低的时候,分布更加尖锐(多样性弱,追求最强棋力)
搜索树会在接下来的自对弈走子中复用,如果孩子节点和落子的位置吻合,它就成为新的根节点,保留子树的所有统计数据,同时丢弃其他的树。如果根的评价值和它最好孩子的评价值都低于 $v_{resign}$ AlphaGo Zero就认输
MCTS搜索总结
与之前的版本的MCTS相比,AlphaGo Zero最大的不同是没有使用走子网络(Rollout),而是使用一个整合的深度神经网络;叶子节点总会被扩展,而不是动态扩展;每一次MCTS搜索线程需要等待神经网络的评估,之前的版本性能评估(evaluate)和返回(backup)是异步的;没有树形策略
至于很重要的一个关键点:每一次模拟的中的叶子节点L的深度
【个人分析】是由时间来决定,根据论文提到的数据,0.4秒执行1600次模拟,多线程模拟,在时限内能走到的深度有多深就是这个叶子节点。可以类比为AlphaGo 1.0中的局面函数(用来判断某个局面下的胜率的),也就是说不用模拟到终盘,在叶子节点的状态下,使用深度神经网的输出 $v$ 来判断现在落子的棋手的胜率
网络结构
网络输入数据
输入数据的维度 19×19×17,其中存储的两个值0/1,$X_t^i = 1$表示这个交叉点有子,$0$ 表示这个交叉点没有子或是对手的子或 $t<0$。使用 $Y_t$ 来记录对手的落子情况。
从状态 $\vec s$ 开始,记录了倒退回去的15步,双方棋手交替。最后一个19×19的存储了前面16步每一个状态对应的棋子的黑白颜色。1黑0白
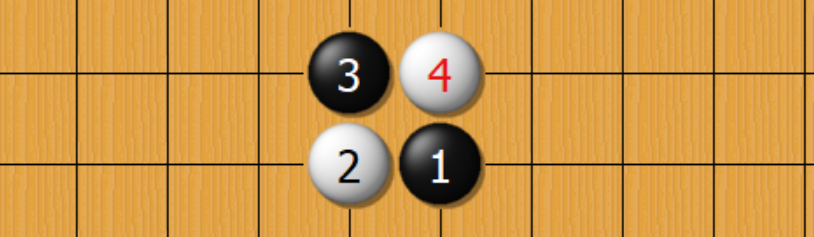
【个人理解】为了更加直观的解释,如果是上面的局部棋盘状态 $\vec s$,接下里一步是黑棋落子,走了4步,那么输入数据是什么样的呢?
$$ \mathbf X_2= \begin{pmatrix} & \vdots & \vdots & \\ \cdots & 0 & 1 & \cdots \\ \cdots & 1 & 0 & \cdots \\ & \vdots & \vdots &\end{pmatrix} \mathbf Y_2= \begin{pmatrix} & \vdots & \vdots & \\ \cdots & 1 & 0 & \cdots \\ \cdots & 0 & 1 & \cdots \\ & \vdots & \vdots &\end{pmatrix} \\ \mathbf X_1= \begin{pmatrix} & \vdots & \vdots & \\ \cdots & 0 & 0 & \cdots \\ \cdots & 1 & 0 & \cdots \\ & \vdots & \vdots &\end{pmatrix} \mathbf Y_1= \begin{pmatrix} & \vdots & \vdots & \\ \cdots & 0 & 0 & \cdots \\ \cdots & 0 & 1 & \cdots \\ & \vdots & \vdots &\end{pmatrix} \\ \mathbf C = \begin{pmatrix} & \vdots & \vdots & \\ \cdots & 1 & 0 & \cdots \\ \cdots & 0 & 1 & \cdots \\ & \vdots & \vdots &\end{pmatrix} $$同理,如果有8步的话,也就是16个对应的 $X$ 和 $Y$ 加一个 $C$ 来表示现在的棋盘状态(注意,这里面包含的历史状态)。这里的数据类型是Boolean,非常高效,并且表达的信息也足够
至于使用八步的原因。个人理解,一方面是为了避免循环劫,另一方面,选择八步也可能是性能和效果权衡的结果(从感知上来说当然信息记录的越多神经网络越强,奥卡姆剃刀定理告诉我们,简单即有效,一味的追求复杂,并不是解决问题的最佳途径)
深度神经网结构
整个残差塔使用单独的卷机模块组成,其中包含了19或39个残差模块,详细结构参数如下图所示
过了深度卷积神经网络后接策略输出与评估值输出,详细结构参数如下图所示
数据集
图5更多细节
总结与随想
AlphaGo Zero = 启发式搜索 + 强化学习 + 深度神经网络,你中有我,我中有你,互相对抗,不断自我进化。使用深度神经网络的训练作为策略改善,蒙特卡洛搜索树作为策略评价的强化学习算法
之后提出一些我在看论文时带着的问题,最后给出我仔细看完每一行论文后得出的回答,如有错误,请批评指正!
问题与个人答案
训练好的Alpha Zero在真实对弈时,在面对一个局面时如何决定下在哪个位置?
评估器的落子过程即最终对弈时的落子过程(自对弈中的落子就是真实最终对局时的落子方式):使用神经网络的输出 $\mathbf p$ 作为先验概率进行MCTS搜索,每步1600次(最后应用的版本可能和每一步的给的时间有关)模拟,前30步采样落子,剩下棋局使用最多访问次数来落子,得到 $\boldsymbol \pi$ ,然后选择落子策略中最大的一个位置落子
AlphaGo Zero的MCTS搜索算法和和上个版本的有些什么区别?
最原始MCTS解析,AlphaGo Lee加上策略函数和局面函数改进后的MCTS解析
对于AlphaGo Zero来说
- 最大的区别在于,模拟过程中依据神经网络的输出 $\mathbf p$ 的概率分布采样落子。采样是关键词,首先采样保证一定的随机特性,不至于下的步数过于集中,其次,如果模拟的盘数足够多,那这一步就会越来越强
- 其次,在返回(Bakcup)部分每一个点的价值(得分),使用了神经网络的输出 $v$。这个值也是策略评估的重要依据
AlphaGo Zero 中的策略迭代法是如何工作的?
策略迭代法(Policy Iteration)是强化学习中的一种算法,简单来说:以某种策略( $\pi_0$ )开始,计算当前策略下的价值函数( $v_{\pi_0}$ );然后利用这个价值函数,找到更好的策略(Evaluate和Improve);接下来再用这个更好的策略继续前行,更新价值函数……这样经过若干轮的计算,如果一切顺利,我们的策略会收敛到最优的策略( $\pi_*$ ),问题也就得到了解答。
$$ \pi_0 \xrightarrow{E} v_{\pi_0} \xrightarrow{I} \pi_1 \xrightarrow{E} v_{\pi_1} \xrightarrow{I} \pi_2 \xrightarrow{E} \cdots \xrightarrow{I} \pi_* \xrightarrow{E} v_* $$对于AlphaGo Zero来说,详细可见论文,简单总结如下
- 策略评估过程,即使用MCTS搜索每一次模拟的对局胜者,胜者的所有落子($\vec s$)都获得更好的评估值
- 策略提升过程,即使用MCTS搜索返回的更好策略 $\boldsymbol \pi$
- 迭代过程,即神经网络输出 $\mathbf p$ 和 $v$ 与策略评估和策略提升返回值的对抗(即神经网络的训练过程)
总的来说,有点像一个嵌套过程,MCST算法可以用来解决围棋问题,这个深度神经网络也可以用来解决围棋问题,而AlphaGo Zero将两者融合,你中有我,我中有你,不断对抗,不对自我进化
AlphaGo Zero 最精彩的部分哪部分?
$$ l = (z - v)^2 - \boldsymbol {\pi}^T \log(\mathbf p) + c \Vert \theta \Vert ^2 $$毫无悬念的,我会选择这个漂亮的公式,看懂公式每一项的来历,即产生的过程,就读懂了AlphaGo Zero。这个公式你中有我,我中有你,这是一个完美的对抗,完美的自我进化
第二我觉得很精彩的点子是将深度神经网络作为一个模块嵌入到了强化学习的策略迭代法中。最关键的是,收敛速度快,效果好,解决各种复杂的局面(比如一个关于围棋棋盘的观看角度可以从八个方向来看的细节处理的很好,又如神经网络的输入状态选择了使用历史八步)
随想和评论
- 不是无监督学习,带有明显胜负规则的强化学习是强监督的范畴
- 无需担心快速的攻克其他领域,核心还是启发式搜索
- 模型简约漂亮,充满整合哲学的优雅,可怕的是效果和效率也同样极高
- AlphaGo项目在经历了把书读厚的过程后,已经取得了瞩目的成就依旧不满足现状,现通过AlphaGo Zero把书读薄,简约而不简单,大道至简,九九归一,已然位列仙班了
随着AlphaGo Zero的归隐,DeepMind已经正式转移精力到其他的任务上了。期待这个天才的团队还能搞出什么大新闻!
对于围棋这项运动的影响可能是:以后的学围棋手段会发生变化,毕竟世界上能复现AlphaGo Zero的绝对很多,那么AlphaGo Zero的实力那就是棋神的感觉,向AlphaGo Zero直接学习不是更加高效嘛?另,围棋受到的关注也应该涨了一波,是利好
感觉强化学习会越来越热,对于和环境交互这个领域,强化学习更加贴近于人类做决策的学习方式。个人预测,强化学习会在未来会有更多进展!AlphaGo Zero 可能仅仅是一个开头
以上!鞠躬!
