【阅读时间】20min 4589 words
【内容简介】从【直观理解】线性代数的本质笔记出发,继续讨论几个线性代数中的概念,正交,正规,正定及转置的直观解释。旨在能帮助读者在看完后不会忘记什么是正交矩阵,什么是正规矩阵,转置部分进行了深入挖掘,希望找出一些几何直观的解释
在之前的【直观理解】线性代数的本质的笔记中,详细讨论了特征值与特征向量的几何直观意义
起初,研究线性代数,也是因为深入了解矩阵(变换)对机器学习中的很多优美公式的推导和理解有帮助。上篇笔记中,3B1B团队的讲解内容中没有涉及几个线性代数中的概念,且这些概念在做矩阵分解时会被用到。以上一篇笔记中的直观理解为基础(矩阵 = 变换)在这里做一个整理和记录
正交矩阵
可能很多人已经有一个概念:正交(Orthogonal) = 垂直。但我们知道,正交的一定垂直,垂直的不一定正交(比如空间中两个不相交直线垂直)。提及垂直,首先出现你脑海中的特点是什么呢?我想是勾股数 $a^2 + b^2 = c^2$ , 还有 $\cos (\frac {\pi}{2}) = 1$
那什么是正交矩阵呢?在讲这个概念之前,变换中有一种特殊变换:旋转变换。这种变换除了原点外没有特征向量,特征值恒为1,不对网格进行伸缩。或者说,这个变换保证了新列空间内和原列空间内所有对应向量的长度不变
三维情况下,单位矩阵(对角线为1,其他为0,即基向量构成的矩阵)$\mathbf E = \left [ \begin{smallmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0&0&1 \end{smallmatrix} \right ]$ 如下图所示
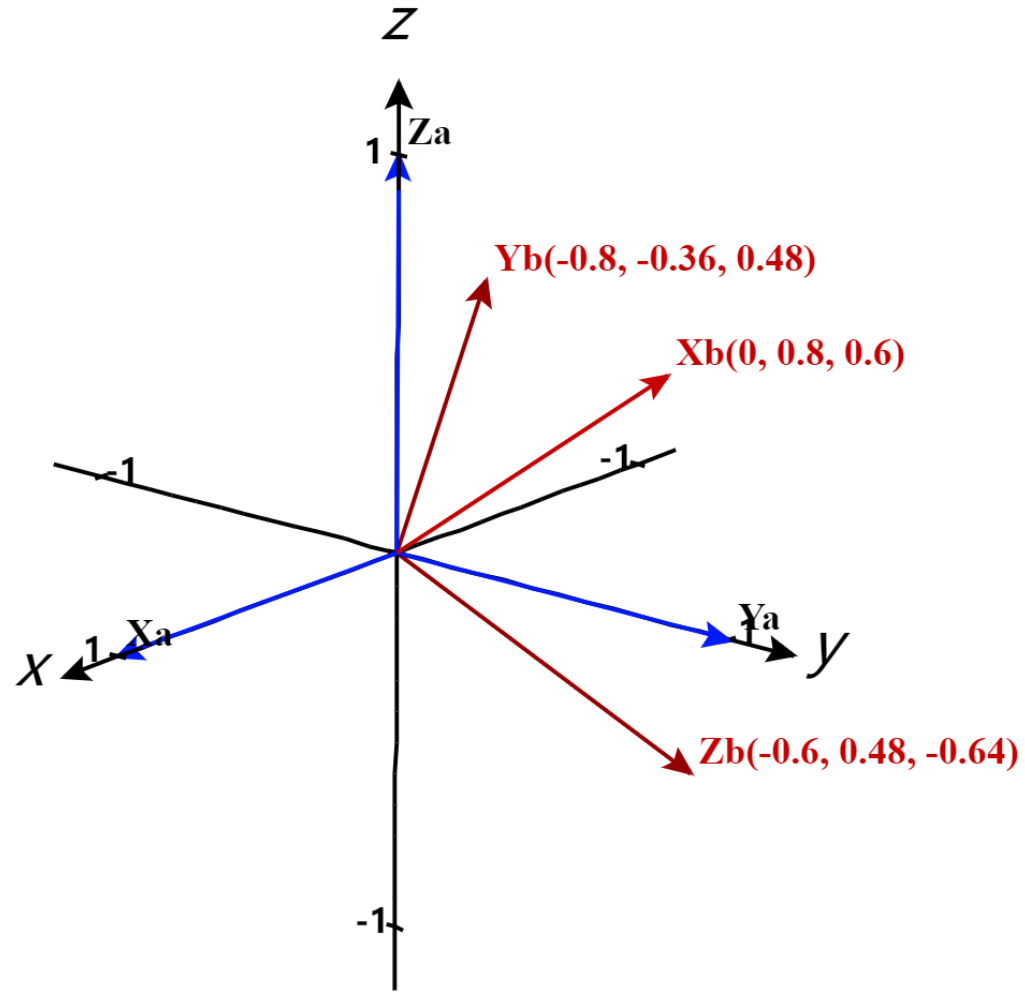
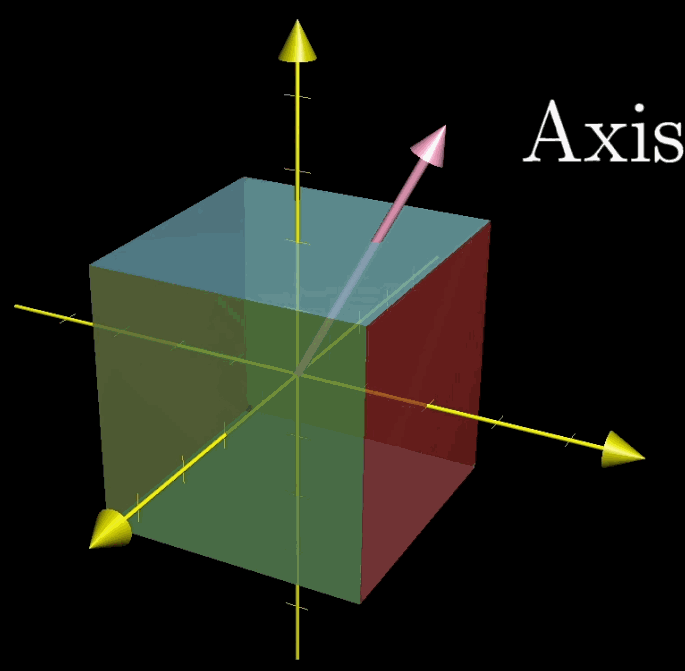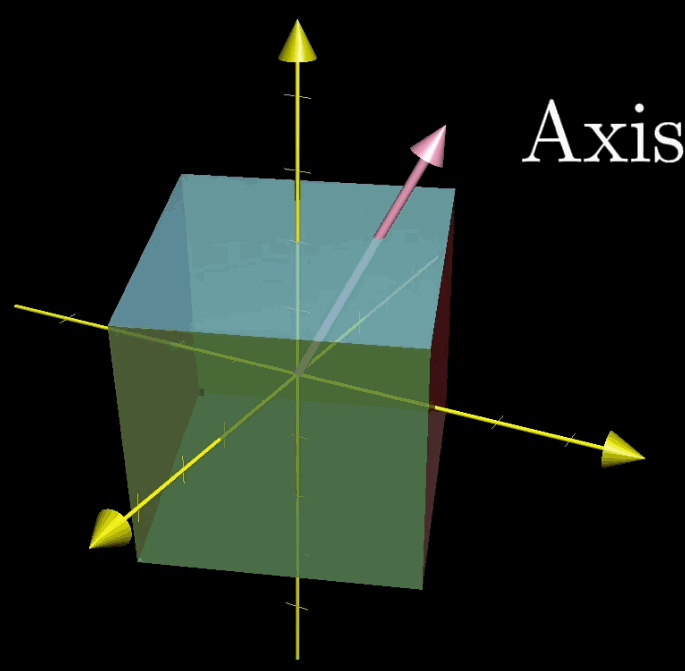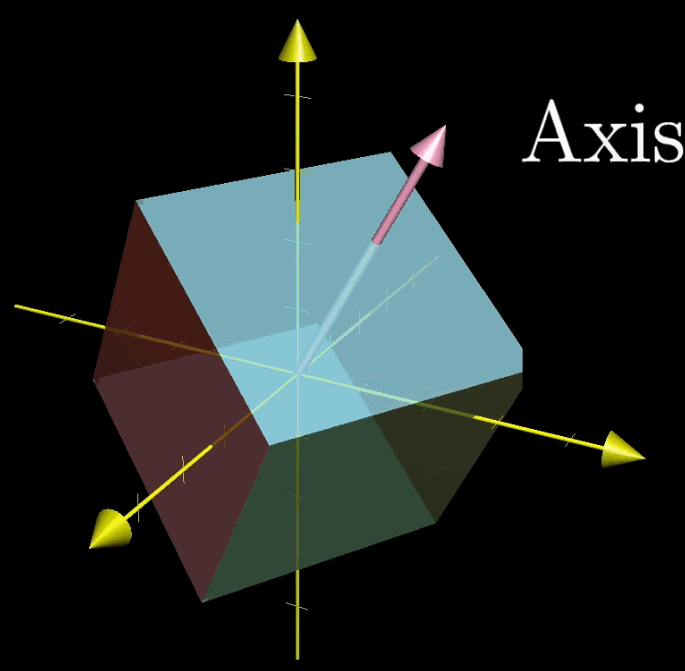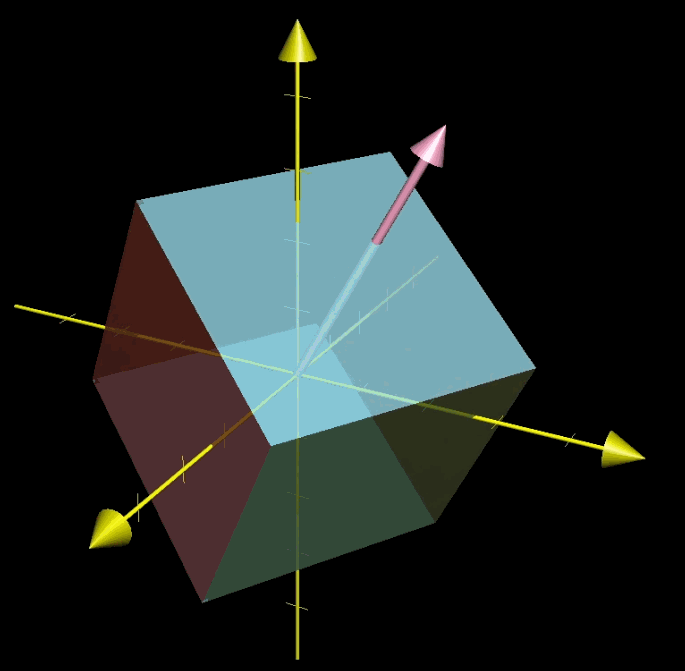
$\mathbf E$ 中的三个基向量分别记为 $\mathbf {X_a}= \left [ \begin{smallmatrix} 1 \\ 0 \\ 0 \end{smallmatrix} \right ] $ ,$\mathbf {Y_a} = \left [ \begin{smallmatrix} 0 \\ 1 \\ 0 \end{smallmatrix} \right ] $,$\mathbf {Z_a} = \left [ \begin{smallmatrix} 0 \\ 0 \\ 1 \end{smallmatrix} \right ] $ ,用下标
a来表示。之后对这个矩阵 $\mathbf E$ 应用一个旋转变换,以 $(0,-0.6,0.8)$ 为旋转轴,转90°。得到三个新的向量,用下标b来表示,记为 $\mathbf {X_b}= \left [ \begin{smallmatrix} 0 \\ 0.8 \\ 0.6 \end{smallmatrix} \right ] $ ,$\mathbf {Y_b} = \left [ \begin{smallmatrix} -0.8 \\ -0.36 \\ 0.48 \end{smallmatrix} \right ] $,$\mathbf {Z_b} = \left [ \begin{smallmatrix} -0.6 \\ 0.48 \\ -0.64 \end{smallmatrix} \right ] $
根据基变换原理,易得旋转变换的矩阵表达式 $\mathbf R = \left [ \begin{smallmatrix} 0&-0.8 &-0.6 \\ 0.8&-0.36&0.48 \\ 0.6&0.48&-0.64 \end{smallmatrix} \right ]$ 计算得特征向量为 $(0,-0.75,1)$,发现这条向量即旋转轴!
此时我们考虑从 $\mathbf R$矩阵下变到 $\mathbf E$的变换矩阵是多少,即求 $\mathbf R$ 矩阵的逆
$$ \mathbf R^{-1} = \left [ \begin{matrix} 0 & 0.8 & 0.6 \\-0.8 & -0.36 & 0.48 \\-0.6 & 0.48 & -0.64 \end{matrix}\right] $$观察形式大家就可以发现一个有趣的特点 $\mathbf R^{-1} = \mathbf R^T$
正交矩阵有一个几何直观的特点,表示一个旋转变换,并且矩阵的逆和矩阵的转置相等
正定与半正定矩阵
根据特征值和特征向量这篇笔记中的内容,我们知道特征值是对一个变换(矩阵)特性的有力表征,公式 $\mathbf A \mathbf{\vec v} = \lambda \mathbf{\vec v}$ 表示了变换中被留在张成空间内的向量就是特征向量的符号表达,其中 $\vec v$ 是特征向量,$\lambda$ 即特征值
我们对上式进行一些数学恒等变换,左乘 $\vec v^T$,得到
$$ \vec v^T \mathbf A \vec v = \vec v^T \lambda \vec v = \lambda \vec v^T \vec v \tag{2-1} $$此时我们会发现一些巧合,先来看看正定矩阵的正规定义:若一个 n×n的矩阵 $\mathbf M$ 是正定的,当且仅当队友所有的非零实系数的向量 $\vec v$,都有 $\vec v^T \mathbf M \vec v > 0$
我们暂时不考虑复数情况(在机器学习预见复数域的内容较少),结合上面的二公式,发现保证 $\vec v^T \mathbf M \vec v > 0$ 即使得 $\lambda \vec v^T \vec v>0$,其中 $\vec v^T \vec v$一定大于等于0(由于 $\vec v$ 是一个1×n的向量,转置进行矩阵相乘实际效果计算元素的平方和),所以可以推出即正定矩阵就是使得特征值大于0
再回到正定矩阵的定义公式 $\vec x^T \mathbf M \vec x > 0$,我们已经有深刻的理解 $\mathbf M \vec x$ 表示对向量 $\vec x$ 进行变换,记变换后的向量为 $\vec y = \mathbf M \vec x$ ,则我们可以把正定矩阵的公式写成
$$ \vec x^T \vec y > 0 \tag{2-2} $$这个公式是不是很熟悉呢?它是两个向量的内积,对于内积,有公式:
$$ \cos(\theta) = \frac{\vec x^T \vec y}{\Vert \vec x \Vert * \Vert \vec y \Vert} \hat {\jmath} $$$\Vert \vec x \Vert \; \Vert \vec y \Vert$ 表示 $\vec x$ 和 $\vec y$的长度,$\theta$ 是它们之间的夹角。根据2-2式,可以得到 $\cos(\theta) > 0$,即它们之间的夹角小于90度
总结:如果说一个矩阵正定,则表示,一个向量经过此矩阵变换后的向量与原向量夹角小于90度
当然,加一个【半】字,是指这个小于变成小于等于
正规矩阵
矩阵中还有一张形状特殊的矩阵,被称为正规矩阵,定义为:如果矩阵 $\mathbf A$ 满足 $\mathbf A^T \mathbf A = \mathbf A \mathbf A^T$
更多的,如果矩阵 $\mathbf U$ 满足 $\mathbf U^T \mathbf U = \mathbf U \mathbf U^T = \mathbf I$,其中 $\mathbf I$ 是单位矩阵,则称矩阵 $\mathbf U$ 为酉矩阵
从变换的角度来看正规矩阵,先做一个变换 $\mathbf A$ 再做一个变换 $\mathbf A^T$。并且交换两个矩阵的位置,最终结果相同
矩阵的转置
什么是转置
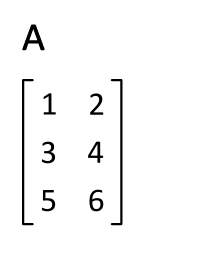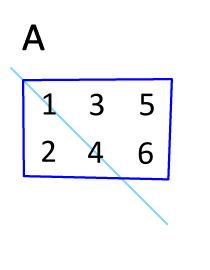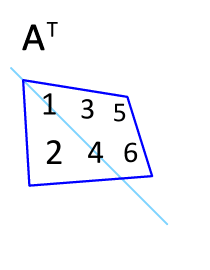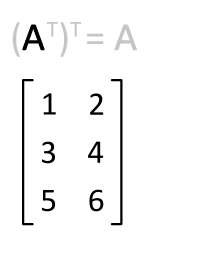
在前面的三个描绘矩阵不同矩阵的概念中,多次使用了转置的概念。从矩阵形态的角度看,转置是将 $\mathbf A$ 的所有元素关于一条从第1行第1列元素出发的向右下方45度的射线作镜面翻转(下面的动图更加直观)
那么,从矩阵是表示变换的集合角度如何理解转置呢?
为什么转置
试图从另一个角度来理解其实也是为了回答另一个问题:为什么要定义转置这种操作呢?你可能会说,这就是一个【对角线镜像对称交换的操作】,从形式上来理解对一般人已完全足够。
这里要深究的原因也只是为了克服在学习机器学习的过程中,公式里若出现转置符号,无法完全理解带来的生涩感(俗称强迫症),对博主来说,一个直接动机源于SVD算法
首先,考虑矩阵的列向量有具体的列空间的含义(对应 $\hat {\imath}$ 和 $\hat {\jmath}$ 的变换位置),若进行转置操作,列空间的性质会被完全破坏,或者说,转换成了一个新的列空间
非方阵
考虑矩阵转置的几何含义是无意义的,或者说,对出现过矩阵转置的公式的进一步理解是没有帮助的
特别的,如果是向量形式(1×n的矩阵),转置很多时候出现,是为了进行二次型运算(即平方运算),设 $\mathbf x = \{x_1, x_2,\ldots, x_n\}$ 是一个1×n的矩阵
很多机器学习的教材中这里会是列矩阵,因为要切合列空间的概念。对于机器学习来说,这里的 $x_1$ 代表的数据的特征维度
计算二次型: $\mathbf x \mathbf x^T = x_1^2 + x_2^2 + \ldots + x_n^2$ ,记过为一个数,表示的是距离
方阵
从列空间的概念,转置是一种非常特殊的旋转。这种旋转结合了横向镜面等特性,详细可以参看下图
从这幅图可以看出,如果想从几何变换的角度(类似3b1b的方法)来理解转置相当困难。此时,需要考虑换一种思考角度,性质和数学计算(这可能也是解决一个数学问题最常用的两种手段,性质寻找共性,并推广演绎,数学计算导出同样问题的不同表现形式,并总结规律)
性质找规律
首先先用一个简单的例子,二维可视化,并寻找规律,得到下面图像
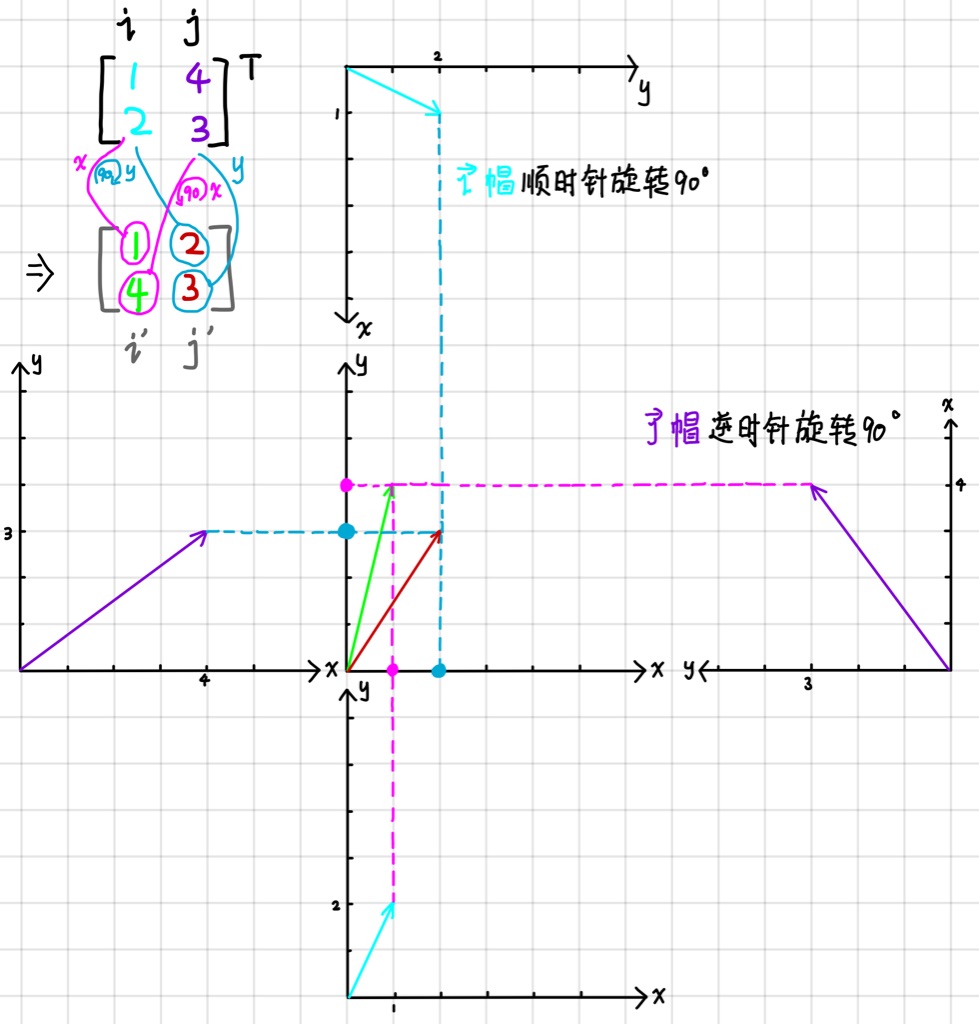
观察得到,和旋转有一定的关系的,但是其实这个几何意义已经十分抽象了,为了追根之底,从数学的角度进行一些更有意思的探究
数学计算
为了发掘 $\mathbf A$ 和 $\mathbf A^T$ 之间的关系,我们可以设有转换矩阵 $\mathbf T$,其描述了从 $\mathbf A$ 到 $\mathbf A^T$ 的变换,写成公式为:
$$
\mathbf T \mathbf A = \mathbf A^{T} \tag 1
$$
同时我们假设 $\mathbf A$ 是一个2×2的矩阵,如下所示所示(列的不同为字母的不同a和b,行的不同为小标的1和2)
保证变换不会压缩维度,即 $det(\mathbf A) \neq 0$,利用(1)式,未知数,消元计算后,可以算出 $\mathbf T$,其中 $det(\mathbf A) = a_1b_2 - b_1a_2$
$$ \mathbf T = \frac{1}{det(\mathbf A)} \begin{bmatrix} a_{1} b_{2} - a_{2}^2 & a_{1} (a_{2} - b_{1}) \\ b_{2} (b_{1} - a_{2}) & a_{1} b_{2} - b_{1}^2 \\ \end{bmatrix} \tag{3} $$前面的 $\frac{1}{det(\mathbf A)}$ 作为一个常数,保证了 $det(\mathbf A^{T})=det(\mathbf A)$,将后面关键的变换矩阵写成
$$ \mathbf T' = \begin{bmatrix} a_{1} b_{2} - a_{2}^2 & a_{1} (a_{2} - b_{1}) \\ b_{2} (b_{1} - a_{2}) & a_{1} b_{2} - b_{1}^2 \\ \end{bmatrix} \tag {4} $$把 (4)式进行整理,也写成矩阵相乘的形式,得到下式
$$ \mathbf T'=\begin{bmatrix} \begin{bmatrix} a_{1} & a_{2} \\ \end{bmatrix} \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} & \begin{bmatrix} a_{1} & a_{2} \\ \end{bmatrix} \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \\ \begin{bmatrix} b_{1} & b_{2} \\ \end{bmatrix} \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} & \begin{bmatrix} b_{1} & b_{2} \\ \end{bmatrix} \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \\ \end{bmatrix} \tag{5} $$对于 $\mathbf A$ 的列空间来说,有 $\mathbf a = \left [ \begin{smallmatrix} a_1 \\ a_2 \end{smallmatrix} \right ]$ 和 $\mathbf b = \left [ \begin{smallmatrix} b_1 \\ b_2 \end{smallmatrix} \right ]$ 观察到 $\mathbf T$ 中包含列空间的两个项,把 $\mathbf T’$ 整理得
$$ B'=\begin{bmatrix} {\mathbf a}^{T} \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} & {\mathbf a}^{T} \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \\ {\mathbf b}^{T} \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} & {\mathbf b}^{T} \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \\ \end{bmatrix}= \begin{bmatrix} {\mathbf a}\cdot \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} & {\mathbf a}\cdot \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \\ {\mathbf b}\cdot \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} & {\mathbf b}\cdot \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \\ \end{bmatrix} \tag{6} $$令 $\mathbf c = \begin{bmatrix}b_{2} \\ -a_{2} \\ \end{bmatrix} $ $\mathbf d = \begin{bmatrix}-b_{1} \\ a_{1} \\ \end{bmatrix} $ ,观察后发现规律:
- $\mathbf c$ 变换到 $\mathbf A^T_{\hat {\jmath}}$ 为逆时针旋转90°
- $\mathbf d$ 变换到 $\mathbf A^T_{\hat {\imath}}$ 为顺时针旋转90°
$\mathbf c$ 和 $\mathbf d$ 组成的列空间设为 $\mathbf C$,写成公式为
$$ \mathbf C = \begin{bmatrix}\mathbf c & \mathbf d\end{bmatrix} = \begin{bmatrix} b_2 & -b_1 \\ -a_2 & a_1\end{bmatrix} \tag{7} $$将(7)式左乘 $\mathbf A$ 得到下式
$$ \mathbf A\mathbf C= \begin{bmatrix} a_{1} & b_{1} \\ a_{2} & b_{2} \\ \end{bmatrix} \cdot \begin{bmatrix} b_{2} & -b_{1} \\ -a_{2} & a_{1} \\ \end{bmatrix} = \begin{bmatrix} det(\mathbf A) & 0 \\ 0 & det(\mathbf A) \\ \end{bmatrix} =det(\mathbf A) \mathbf I \tag{8} $$再将(8)式所有乘以 $\mathbf A$ 的逆矩阵 $\mathbf A^{-1}$ 得到
$$
\mathbf C = \mathbf A^{-1} det(\mathbf A) \tag{9}
$$
所以,构造的这个 $\mathbf C$ 矩阵和 $\mathbf A$ 矩阵的逆矩阵有关
另外,(4)式,即 $\mathbf T’$ 矩阵还可以被写成
$$ \mathbf T'=\begin{bmatrix} \begin{bmatrix} \begin{bmatrix} a_{1} & b_{1} \\ a_{2} & b_{2} \\ \end{bmatrix} & \begin{bmatrix} b_{2} \\ -a_{2} \\ \end{bmatrix} \end{bmatrix} \\ \begin{bmatrix} \begin{bmatrix} a_{1} & b_{1} \\ a_{2} & b_{2} \\ \end{bmatrix} & \begin{bmatrix} -b_{1} \\ a_{1} \\ \end{bmatrix} \end{bmatrix} \end{bmatrix} = \begin{bmatrix} \begin{bmatrix} \begin{bmatrix} a_{1} & b_{1} \\ a_{2} & b_{2} \\ \end{bmatrix} & \mathbf c \end{bmatrix} \\ \begin{bmatrix} \begin{bmatrix} a_{1} & b_{1} \\ a_{2} & b_{2} \\ \end{bmatrix} & \mathbf d \end{bmatrix} \end{bmatrix} \tag{10} $$或者可以写成
$$ \begin{align} \mathbf T' & = \begin{bmatrix} \begin{bmatrix} a_{1} & a_{2} \\ \end{bmatrix} & \begin{bmatrix} b_{2} & -b_{1} \\ -a_{2} & a_{1} \\ \end{bmatrix} \\ \begin{bmatrix} a_{2} & b_{2} \\ \end{bmatrix} & \begin{bmatrix} b_{2} & -b_{1} \\ -a_{2} & a_{1} \\ \end{bmatrix} \\ \end{bmatrix} = \begin{bmatrix} \mathbf a^{T} & \begin{bmatrix} \mathbf c & \mathbf d \\ \end{bmatrix} \\ \mathbf b^{T} & \begin{bmatrix} \mathbf c & \mathbf d \\ \end{bmatrix} \\ \end{bmatrix} \\ & = \begin{bmatrix} \mathbf c^{T}\mathbf C \\ \mathbf d^{T}\mathbf C \\ \end{bmatrix} = det(\mathbf A) \begin{bmatrix} \mathbf a^{T}\mathbf A^{-1} \\ \mathbf b^{T}\mathbf A^{-1} \\ \end{bmatrix} \end{align} \tag{11} $$由 $\mathbf T \mathbf A = \mathbf A^T$ 可得
$$ \mathbf T= \begin{bmatrix} \mathbf a^T \mathbf A^{-1} \\ \mathbf b^T \mathbf A^{-1} \end{bmatrix} \tag{12} $$这时候,可以得出一个结论,矩阵的转置的过程和矩阵的逆是有关系的,是矩阵逆的一个更加复杂的表现形式
有了这个作为基础,考虑一下具有对称性,构造 $\mathbf A \mathbf A^T$,这个复合变换有着很好的对称性和分解性(接下来为了方便,默认非粗体表示的矩阵变换),因为
$$ AA^T = \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2\end{bmatrix}\begin{bmatrix} a_1 & a_2 \\ b_1 & b_2\end{bmatrix} = \begin{bmatrix} a_1^2 + b_1^2 & a_1a_2+b_1b_2 \\ a_1a_2+b_1b_2 & a_2^2 + b_2^2\end{bmatrix} \tag{13} $$考虑任何不进行压缩维度变换的矩阵都可以进行特征分解,则有
$$ AA^{T} = R_{AA^{T}} \Lambda_{AA^{T}} (R^{-1})_{AA^{T}} \tag{14} $$之后左乘(这里补充一下,所有的左乘操作在几何意义上来说,就是附加了一个新的变换)$A^{-1}$,得到
$$ A^{T} = A^{-1} R_{AA^{T}} \Lambda_{AA^{T}} (R^{-1})_{AA^{T}} \tag{15} $$根据之前(1)式的例子进行计算,发现 $R_{AA^{T}} = (R^{-1})_{AA^{T}}$,并且 $R_{AA^T}$ 首先将空间关于 y 轴对称,之后旋转 $\alpha$ 角度,所以假设定义
$$ R_{AA^{T}}^{'} = \begin{bmatrix} cos \alpha & -sin \alpha \\ sin \alpha & cos \alpha \\ \end{bmatrix} \tag{16} $$利用上面的推导,带入(15)式,得到:
$$ A^{T}=A^{-1} R_{AA^{T}}^{'} \begin{bmatrix} -1 & 0 \\ 0 & 1 \\ \end{bmatrix} \Lambda_{AA^{T}} R_{AA^{T}}^{'} \begin{bmatrix} -1 & 0 \\ 0 & 1 \\ \end{bmatrix} \tag{17} $$用更加清晰的符号改写(17)式得到
$$ A^{T}=A^{-1} R_{\alpha} M_y \Lambda R_{\alpha} M_y \tag{18} $$$M_y$ 表示的是关于y轴对称
$R_\alpha$ 表示逆时针旋转 $\alpha$ 度
$\Lambda$ 表示一种伸缩变换
这里的(18式)结论和上面的作图规律,还有(12)式从某种程度上来说有相似的地方
其实应该从矩阵分解的部分来再次思索矩阵转置的意义,可详见什么是PCA,SVD
最终感觉关于转置还是研究的不够透彻,可能需要拔高到另一个层面去理解会更加直观,但是限于水平,只能至此(并不是数学专业的学生)
总结
- $\mathbf A \mathbf A^T$ 的对称特性非常有用
- 正交 = 旋转 = 垂直,并且逆等于转置
- 正规矩阵的定义和转置息息相关,但是从形式上来看,约束条件是逐步变弱的,其实这些特征都是描述了空间一个变换的一些变化模式,比如旋转,伸缩的特殊模式,只需要有一个基本的直观理解,在机器学习领域就已经足够用了
