【阅读时间】7min - 9min
【内容简介】主要解决什么是正则化,为什么使用正则化,如何实现正则化,外加一些对范数的直观理解并进行知识整理以供查阅
Why & What 正则化
我们总会在各种地方遇到正则化这个看起来很难理解的名词,其实它并没有那么高冷,是很好理解的
首先,从使用正则化解决了一个什么问题的角度来看:正则化是为了防止过拟合, 进而增强泛化能力。用白话文转义,泛化误差(generalization error)= 测试误差(test error),其实就是使用训练数据训练的模型在测试集上的表现(或说性能 performance)好不好
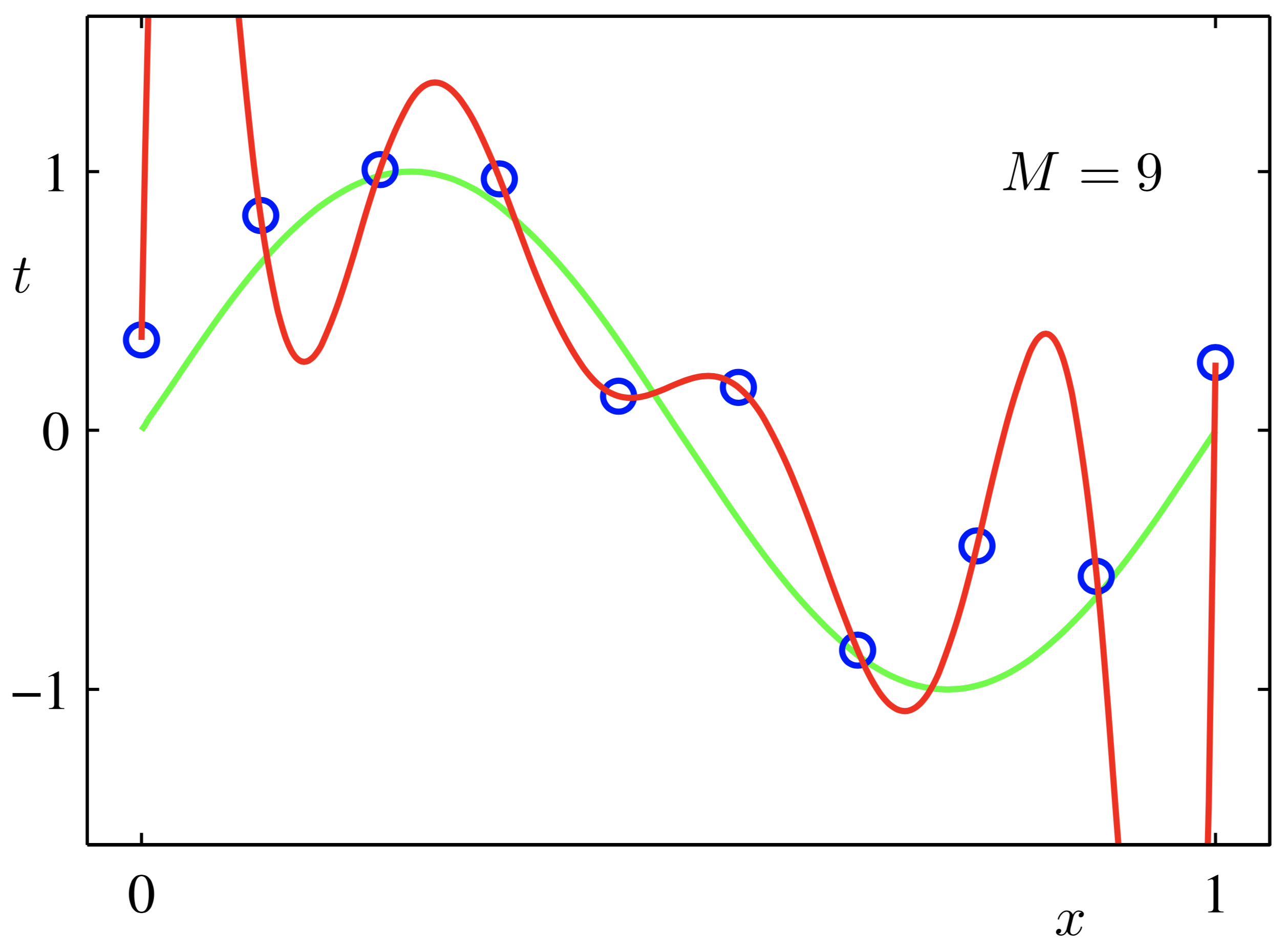
如上图,红色这条“想象力”过于丰富上下横跳的曲线就是过拟合情形。结合上图和正则化的英文 Regularizaiton-Regular-Regularize,直译应该是:规则化(加个“化”字变动词,自豪一下中文还是强)。什么是规则?你妈喊你6点前回家吃饭,这就是规则,一个限制。同理,在这里,规则化就是说给需要训练的目标函数加上一些规则(限制),让他们不要自我膨胀。正则化,看起来,挺不好理解的,追其根源,还是“正则”这两字在中文中实在没有一个直观的对应,如果能翻译成规则化,更好理解。但我们一定要明白,搞学术,概念名词的准确是十分重要,对于一个重要唯一确定的概念,为它安上一个不会产生歧义的名词是必须的,正则化的名称没毛病,只是从如何理解的角度,要灵活和类比。
我的思考模式的中心有一个理念:每一个概念,被定义就是为了去解决一个实际问题(问Why&What),接着寻找解决问题的方法(问How),这个“方法”在计算机领域被称为“算法”(非常多的人在研究)。我们无法真正衡量到底是提出问题重要,还是解决问题重要,但我们可以从不同的解决问题的角度来思考问题。一方面,重复以加深印象。另一方面,具有多角度的视野,能让我们获得更多的灵感,真正做到链接并健壮自己的知识图谱
How 线性模型角度
对于线性模型来说,无论是Logistic Regression、SVM或是简单的线性模型,都有一个基函数 $\phi()$,其中有很多 $\mathbf w$ (参数)需要通过对损失函数 $E()$ 求极小值(或最大似然估计)来确定,求的过程,也就是使用训练集的训练过程:梯度下降到最小值点。最终,找到最合适的 $\mathbf w$ 确定模型。从这个角度来看,正则化是怎么做的呢?
二次正则项
我们看一个线性的损失函数(真实值和预测值的误差)
$$
E(\mathbf w) =\frac{1}{2} \sum_{n=1}^{N}\{t_n-\mathbf w^T \phi (\mathbf x_n)\}^2 \tag{1}
$$
$E(\mathbf w)$ 是损失函数(又称误差函数),
E即Evaluate,有时候写成L即Loss
$t_n$ 是测试集的真实输出,又称目标变量【对应第一幅图中的蓝色点】
$\mathbf w$ 是权重(需要训练的部分,未知数)
$\phi()$ 是基函数,例如多项式函数,核函数
测试样本有n个数据
整个函数直观解释就是误差方差和,$\frac{1}{2}$ 只是为了求导后消去方便计算
加正则化项,得到最终的误差函数(Error function)
$$
\frac{1}{2} \sum_{n=1}^{N}\{t_n-\mathbf w^T \phi (\mathbf x_n)\}^2 + \frac{\lambda}{2} \mathbf w^T \mathbf w \tag{2}
$$
(2)式被称为目标函数(评价函数)= 误差函数(损失函数) + 正则化项
$\lambda$ 被称为正则化系数,越大,这个限制越强
2式对 $\mathbf w$ 求导,并令为0(使误差最小),可以解得
$$ \mathbf w = (\lambda \mathbf I + \Phi^T \Phi)^{-1}\Phi^T\mathbf t $$这是最小二乘法的解形式,所以在题目中写的是从“最小二乘角度”。至于为何正则化项是 $\frac{\lambda}{2} \mathbf w^T \mathbf w$ 在之后马上解释
一般正则项
直观的详解为什么要选择二次正则项。首先,需要从一般推特例,然后分析特例情况的互相优劣条件,可洞若观火。一般正则项是以下公式的形式
$$ \frac{1}{2} \sum_{n=1}^{N}\{t_n-\mathbf w^T \phi (\mathbf x_n)\}^2 + \frac{\lambda}{2} \sum_{j=1}^{M} {\vert w_j \vert}^q \tag{3} $$
M是模型的阶次(表现形式是数据的维度),比如M=2,就是一个平面(二维)内的点
若q=2就是二次正则项。高维度没有图像表征非常难以理解,那就使用二维作为特例来理解。这里令M=2,即 $\mathbf x =\{x_1,x_2\} \;\mathbf w=\{w_1,w_2\}$ ,令q=0.5 q=1 q=2 q=4 有
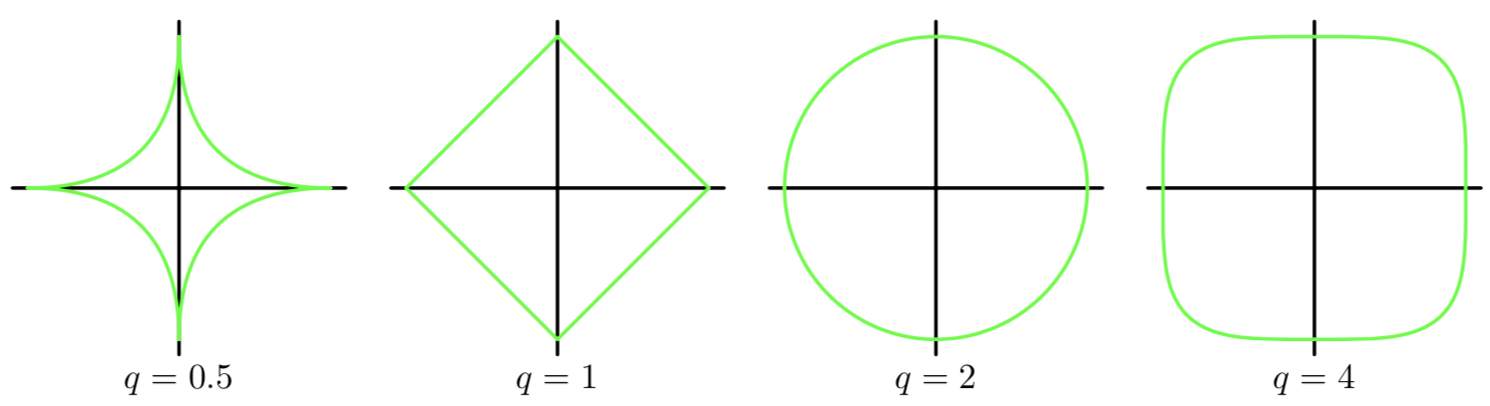
横坐标是$w_1$
纵坐标是$w_2$
绿线是等高线的其中一条,换言之是一个俯视图,而z轴代表的是 $ \frac{\lambda}{2} \sum_{j=1}^{M} {\vert w_j \vert}^q$ 的值
空间想象力不足无法理解的读者希望下方的三维图像能给你一个直观的领悟(与绿线图一一对应)
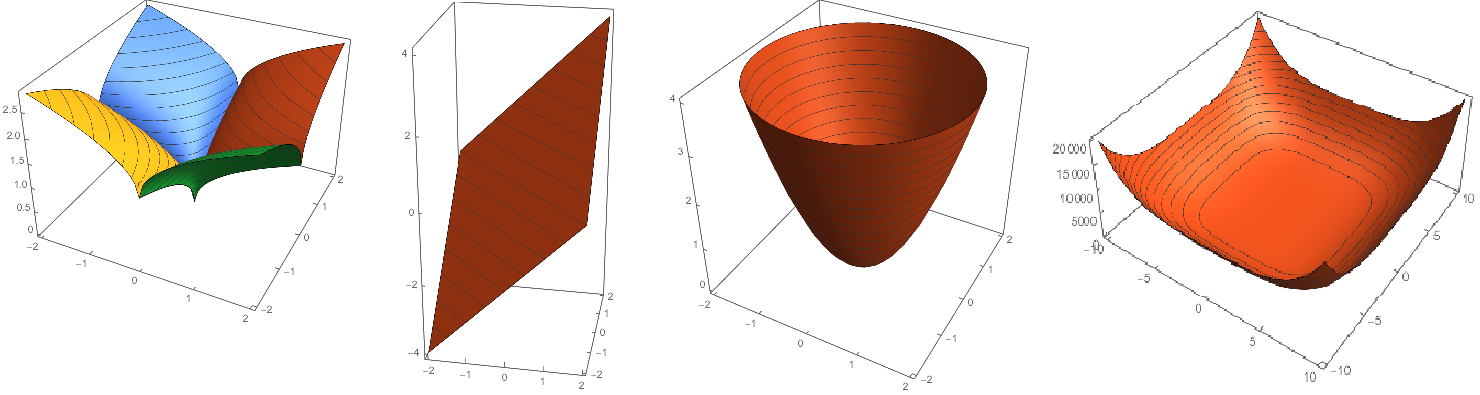
q=2是一个圆非常好理解,考虑 $z = w_1^2 + w_2^2 $ 就是抛物面,俯视图是一个圆。其他几项同理(必须强调俯视图和等高线的概念,z轴表示的是正则项项的值)
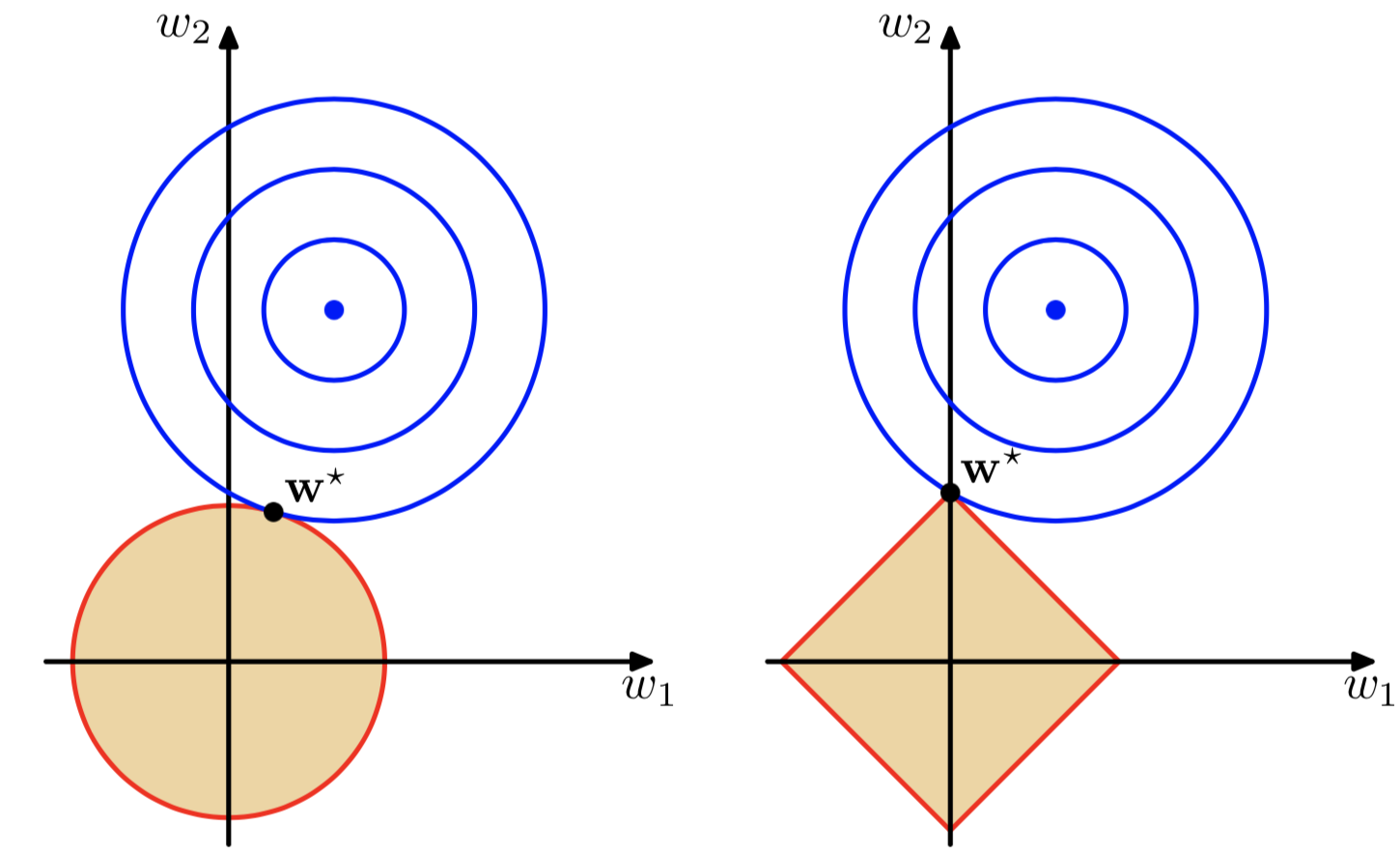
蓝色的圆圈表示没有经过限制的损失函数在寻找最小值过程中,$\mathbf w$的不断迭代(随最小二乘法,最终目的还是使损失函数最小)变化情况,表示的方法是等高线,z轴的值就是 $E(\mathbf w)$
$w^*$ 最小值取到的点
可以直观的理解为(帮助理解正则化),我们的目标函数(误差函数)就是求蓝圈+红圈的和的最小值(回想等高线的概念并参照3式),而这个值通在很多情况下是两个曲面相交的地方
可以看到二次正则项的优势,处处可导,方便计算,限制模型的复杂度,即 $\mathbf w$ 中M的大小,M是模型的阶次,M越大意味着需要决定的权重越多,所以模型越复杂。在多项式模型多,直观理解是每一个不同幂次的 $x$ 前的系数,0(或很小的值)越多,模型越简单。这就从数学角度解释了,为什么正则化(规则化)可以限制模型的复杂度,进而避免过拟合
不知道有没有人发现一次正则项的优势,$w^*$ 的位置恰好是 $w_1=0$ 的位置,意味着从另一种角度来说,使用一次正则项可以降低维度(降低模型复杂度,防止过拟合)二次正则项也做到了这一点,但是一次正则项做的更加彻底,更稀疏。不幸的是,一次正则项有拐点,不是处处可微,给计算带来了难度,很多厉害的论文都是巧妙的使用了一次正则项写出来的,效果十分强大
How 神经网络模型角度
我们已经知道,最简单的单层神经网,可以实现简单的线性模型。而多隐含层的神经网络模型如何来实现正则化?(毕竟神经网络模型没有目标函数)
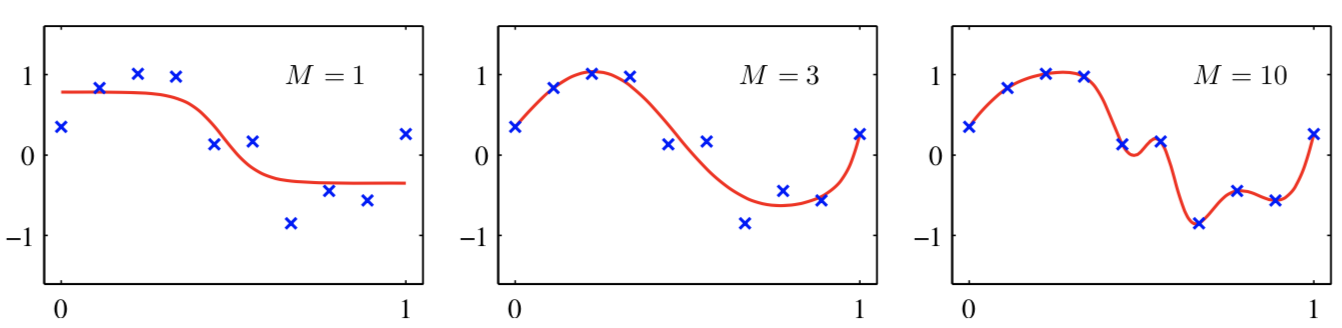
M表示单层神经网中隐含层中的神经元的数量
上图展示了神经网络模型过拟合的直观表示
我们可以通过一系列的推导得知,未来保持神经网络的一致性(即输出的值不能被尺缩变换,或平移变换),在线性模型中的加入正则项无法奏效
所以我们只能通过建立验证集(Validation Set),拉网搜索来确定M的取值(迭代停止的时间),又称为【提前停止】
这里有一个尾巴,即神经网络的不变量(invariance),我们并不希望加入正则项后出现不在掌控范围内的变化(即所谓图像还是那个图像,不能乱变)。而机器学习的其中一个核心目的也是去寻找不同事物(对象)的中包含信息的这个不变量(特征)。卷积神经网络从结构上恰恰实现了这种不变性,这也是它强大的一个原因
范数
我并不是数学专业的学生,但是我发现在讲完线性模型角度后,有几个概念可以很轻松的解答,就在这里献丑把它们串联起来,并做一些总结以供查阅和对照。
我们知道,范数(norm)的概念来源于泛函分析与测度理论,wiki中的定义相当简单明了:范数是具有“长度”概念的函数,用于衡量一个矢量的大小(测量矢量的测度)
我们常说测度测度,测量长度,也就是为了表征这个长度。而如何表达“长度”这个概念也是不同的,也就对应了不同的范数,本质上说,还是观察问题的方式和角度不同,比如那个经典问题,为什么矩形的面积是长乘以宽?这背后的关键是欧式空间的平移不变性,换句话说,就是面积和长成正比,所以才有这个
没有测度论就没有(现代)概率论。而概率论也是整个机器学习学科的基石之一。测度就像尺子,由于测量对象不同,我们需要直尺量布匹、皮尺量身披、卷尺量房间、游标卡尺量工件等等。注意,“尺子”与刻度(寸、米等)是两回事,不能混淆。
范数分为向量范数(二维坐标系)和矩阵范数(多维空间,一般化表达),如果不希望太数学化的解释,那么可以直观的理解为:0-范数:向量中非零元素的数量;1-范数:向量的元素的绝对值;2-范数:是通常意义上的模(距离)
向量范数
关于向量范数,先再把这个图放着,让大家体会到构建知识图谱并串联知识间的本质(根)联系的好处

p-范数
$$ \Vert\mathbf x \Vert_p =(\sum\limits_{i=1}^{N}\vert x_i \vert^p)^{\frac{1}{p}} $$向量元素绝对值的p次方和的 $\frac{1}{p}$ 次幂。可以敏捷的发现,这个p和之前的q从是一个东西,随着p越大,等高线图越接近正方形(正无穷范数);越小,曲线弯曲越接近原点(负无穷范数)
而之前已经说明,q的含义是一般化正则项的幂指数,也就是我们常说的2范数,两者在形式上是完全等同的。结合范数的定义,我们可以解释一般化正则项为一种对待求参数 $\mathbf w$ 的测度,可以用来限制模型不至于过于复杂
$-\infty$-范数
$$ \Vert \mathbf x \Vert_{-\infty} = arg \operatorname*{min}_{i}{\vert x_i \vert} $$所有向量元素中绝对值的最小值
1-范数
$$ \Vert \mathbf x \Vert_1 = \sum\limits_{i=1}^{N}\vert x_i \vert $$向量元素绝对值之和,也称街区距离(city-block)
$$ \begin{matrix} 4 & 3 & 2 & 3 & 4 \\ 3 & 2 & 1 & 2 & 3\\ 2 & 1 & 0 & 1 & 2 \\ 3 & 2 & 1 & 2 &3 \\ 4&3 & 2 &3 &4 \\ \end{matrix} $$2-范数
$\Vert\mathbf x \Vert_2 = \sqrt{\sum\limits_{i=1}^{N} x_i^2}$ :向量元素的平方和再开方。Euclid范数,也称欧几里得范数,欧氏距离$$ \begin{matrix} 2.8&2.2&2&2.2&2.8 \\ 2.2&1.4&1&1.4&2.2 \\ 2&1&0&1&2 \\ 2.2&1.4&1&1.4&2.2 \\ 2.8&2.2&2&2.2&2.8 \\ \end{matrix} $$
$\infty$-范数
$\Vert \mathbf x \Vert_{\infty} = arg \operatorname*{max}_{i}{\vert x_i \vert}$ :所有向量元素中绝对值的最大值,也称棋盘距离(chessboard),切比雪夫距离$$ \begin{matrix} 2 & 3 & 2 & 2 & 2 \\ 2 & 1 & 1 & 1 & 2\\ 2 & 1 & 0 & 1 & 2 \\ 2 & 1 & 1 & 1 &2 \\ 2&2 & 2 &2 &2 \\ \end{matrix} $$
矩阵范数
1-范数
$$ \Vert \mathbf A \Vert_{1} = arg \operatorname*{max}_{1 \leqslant j \leqslant n}\sum\limits_{i=1}^m{\vert a_{i,j} \vert} $$列和范数,即所有矩阵列向量绝对值之和的最大值
$\infty$-范数
$$ \Vert \mathbf A \Vert_{\infty} = arg \operatorname*{max}_{1 \leqslant i \leqslant n}\sum\limits_{j=1}^m{\vert a_{i,j} \vert} $$行和范数,即所有矩阵行向量绝对值之和的最大值
2-范数
$\Vert \mathbf A \Vert_{2} = \sqrt{\lambda_{max}(\mathbf A^* \mathbf A) }$p=2且m=n方阵时,称为谱范数。矩阵 $\mathbf A$ 的谱范数是 $\mathbf A$ 最大的奇异值或半正定矩阵 $\mathbf A^T \mathbf A$ 的最大特征值的平方根
$\mathbf A^*$ 为 $\mathbf A$ 的共轭转置,实数域等同于 $\mathbf A^T$
F-范数
$\Vert \mathbf A \Vert_{F} = \sqrt{ \sum\limits_{i=1}^m \sum\limits_{j=1}^n \vert a_{i,j}\vert^2 }$Frobenius范数(希尔伯特-施密特范数,这个称呼只在希尔伯特空间),即矩阵元素绝对值的平方和再开平方
核范数
$\Vert \mathbf A \Vert_{*} = \sum\limits_{i=1}^n \lambda_i$ :$\lambda_i$ 若 $\mathbf A$ 矩阵是方阵,称为本征值。若不是方阵,称为奇异值,即奇异值/本征值之和
总结
相信每个人在学习过程中都有过看书时,遇到0-范数正则化,或者1-范数正则化,2-范数正则化的表达时很迷惑。写到这里,希望大家能对这些看起来无法理解的晦涩名词有一个融会贯通的理解和感知!
Learning with intuitive and get Insight
以上!鞠躬!
