【阅读时间】8min - 10mun
【内容简介】直观的解读了什么是拉格朗日乘子法,以及如何求解拉格朗日方程,并且给出几个直观的例子,针对不等式约束解读了KKT条件的必要条件和充分条件
What & Why
拉格朗日乘法(Lagrange multiplier)是一种在最优化的问题中寻找多元函数在其变量受到一个或多个条件的相等约束时的求局部极值的方法。这种方法可以将一个有 n 个变量和 k 个约束条件的最优化问题转换为一个解有 n+k 个变量的方程组的解的问题
考虑一个最优化问题
$$ \operatorname*{max}_{x,y} f(x,y) \qquad s.t.\;\; g(x,y)=c $$为了求 $x$ 和 $y$ ,引入一个新的变量 $\lambda$ 称为拉格朗日乘数,再引入朗格朗日函数的极值
$$
\mathcal{L}(x,y,\lambda)=f(x,y)-\lambda \cdot \bigl( g(x,y) - c\bigl) \tag 1
$$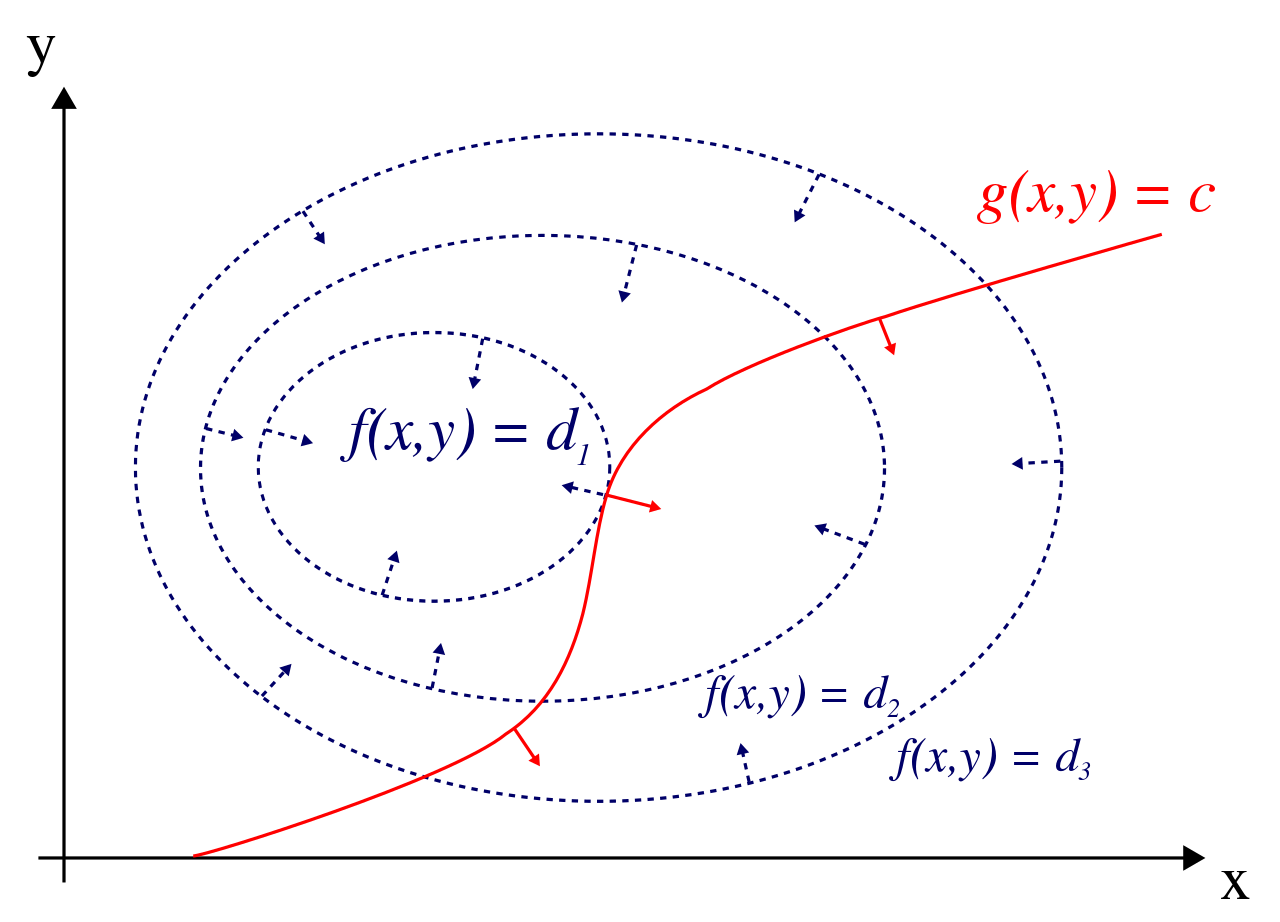
红线表示 $g(x,y) = c$ ,蓝线是 $f(x,y)$ 的等高线,所有箭头表示梯度下降最快的方向。图中红线与等高线相切的位置就是待求的极大值
How
那么如何求这个极值点呢?
单约束
对(1)式直接求微分,并令其为零,计算出鞍点
$$ \nabla_{x,y,\lambda} \mathcal{L}(x,y,\lambda) = 0 $$ 有三个未知数,所以需要3个方程。求 $\lambda$ 的偏微分有 $\nabla_{\lambda} \mathcal{L}(x,y,\lambda) = 0 \implies g(x,y)=0$,则总结得 $$ \nabla_{x,y,\lambda} \mathcal{L}(x,y,\lambda) = 0 \iff \begin{cases} \nabla_{x,y} f(x,y) = \lambda \nabla_{x,y} g(x,y) \\ g(x,y)=0 \end{cases} $$例子1
设一个具体的例子,我们需要求下列问题
$$
\operatorname*{max}_{x,y} f(x,y) = x^2y \qquad s.t.\;\; g(x,y): x^2+y^2-3=0
$$
只有一个约束,使用一个乘子,设为 $\lambda$,列出拉格朗日函数
$$
\mathcal{L}(x,y,\lambda)=f(x,y)-\lambda \cdot \bigl( g(x,y) - c\bigl) = x^2y + \lambda(x^2+y^2-3)
$$
接下来求解上式,分别对三个待求量偏微分
$$
\begin{align}
\nabla_{x,y,\lambda} \mathcal{L}(x,y,\lambda) & = \left( \frac{\partial \mathcal{L}}{\partial x},\frac{\partial \mathcal{L}}{\partial y},\frac{\partial \mathcal{L}}{\partial \lambda}\right)\\
& = (2xy + 2\lambda x, x^2 + 2\lambda y, x^2 + y^2 - 3)
\end{align}
$$
令偏微分分别等于0,得到
$$
\nabla_{x,y,\lambda} \mathcal{L}(x,y,\lambda) = 0 \iff
\begin{cases}
2xy+2\lambda x = 0 \\
x^2 + 2\lambda y = 0 \\
x^2 + y^2 - 3 = 0
\end{cases}
\iff
\begin{cases}
x(y + \lambda) = 0 & (i)\\
x^2 = -2\lambda y & (ii)\\
x^2 +y^2 = 3 & (iii)
\end{cases}
$$
根据上式,我们可以解得 $\mathcal{L}$:
$$
(\pm \sqrt{2},1,-1 ); (\pm \sqrt{2},-1,1 );(0,\pm \sqrt{3},0)
$$
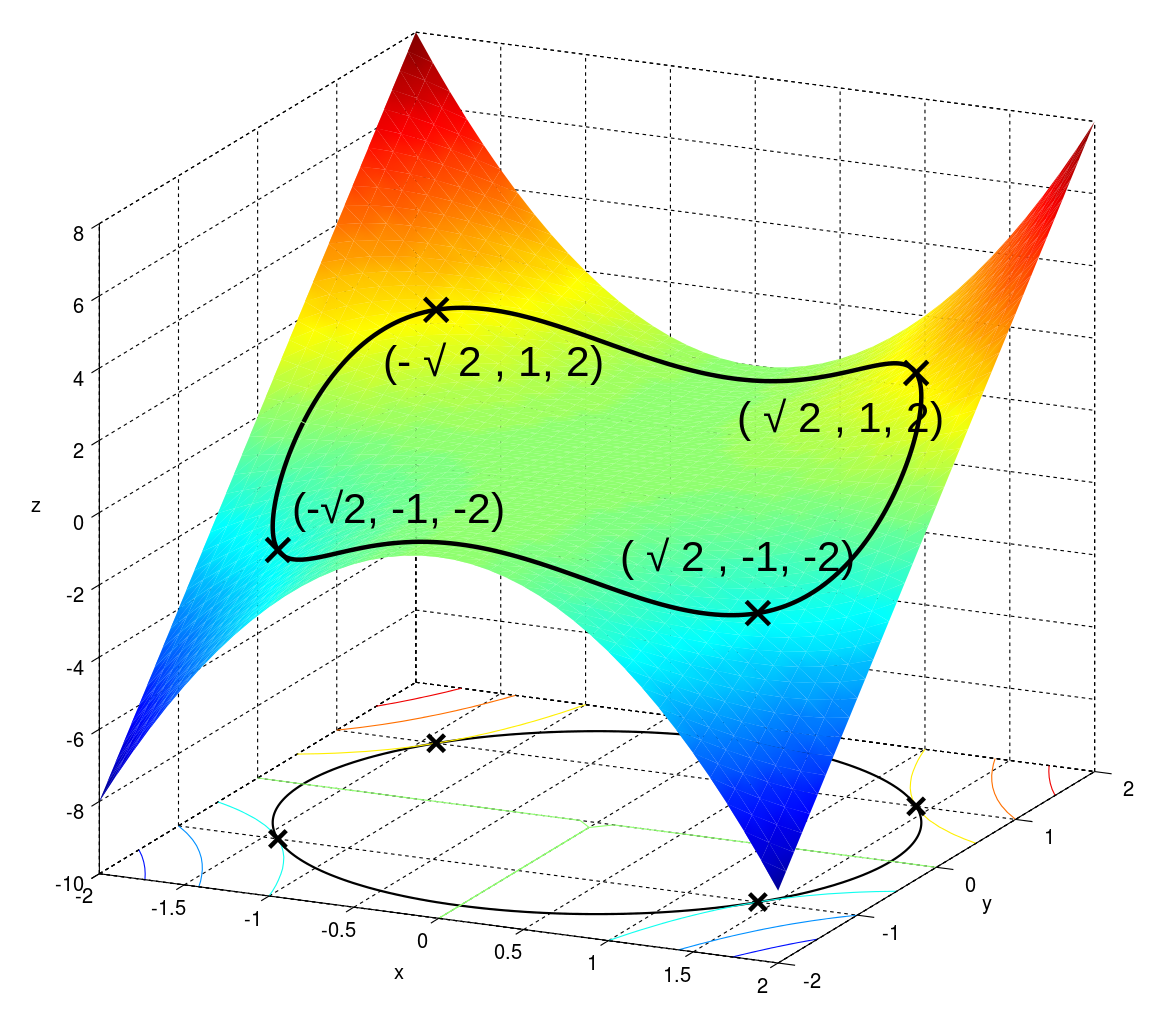
根据几个不同的解带入 $f(x,y)$ 得到,2,-2,0,也就是我们需要的最大值,最小值,对应的直观图像解释如下图所示(非常直观的展现约束和等高线的含义)
例子2
关于拉格朗日乘子法的应用,有一个十分著名的:求离散概率分布 $p_1,p_2,\cdots,p_n$ 的最大信息熵
$$
f(p1,p2,\cdots,p_n) = - \sum_{j=1}^n p_j log_2{p_j} \\
s.t. \quad g(p1,p2,\cdots,p_n) = \sum_{k=1}^n p_k = 1 \text{(概率和为1)}
$$
单约束问题,引入一个乘子 $\lambda$ ,对于 $k \in [1,n]$ ,要求
$$
\frac{\partial}{\partial p_k} (f + \lambda(g - 1)) = 0
$$
将 $f$ 和 $g$ 带入有
$$
\frac{\partial}{\partial p_k} \left( -\sum_{k=1}^np_klog_2{p_k} + \lambda (\sum_{k=1}^n p_k - 1)\right) = 0
$$
计算这 n 个等式的偏微分,我们可以得到:
$$
-\left( \frac{1}{\ln(2)} + log_2p_k \right) + \lambda = 0
$$
这说明所有的 $p_i$ 都相等,所以得到 $p_k = \frac{1}{n}$
我们可以得到一个结论是:均匀分布的信息熵是最大的
多约束
既然可以解决单约束,继续思考一下多约束情况的直观表现,假设我们的约束是两条线,如下图所示
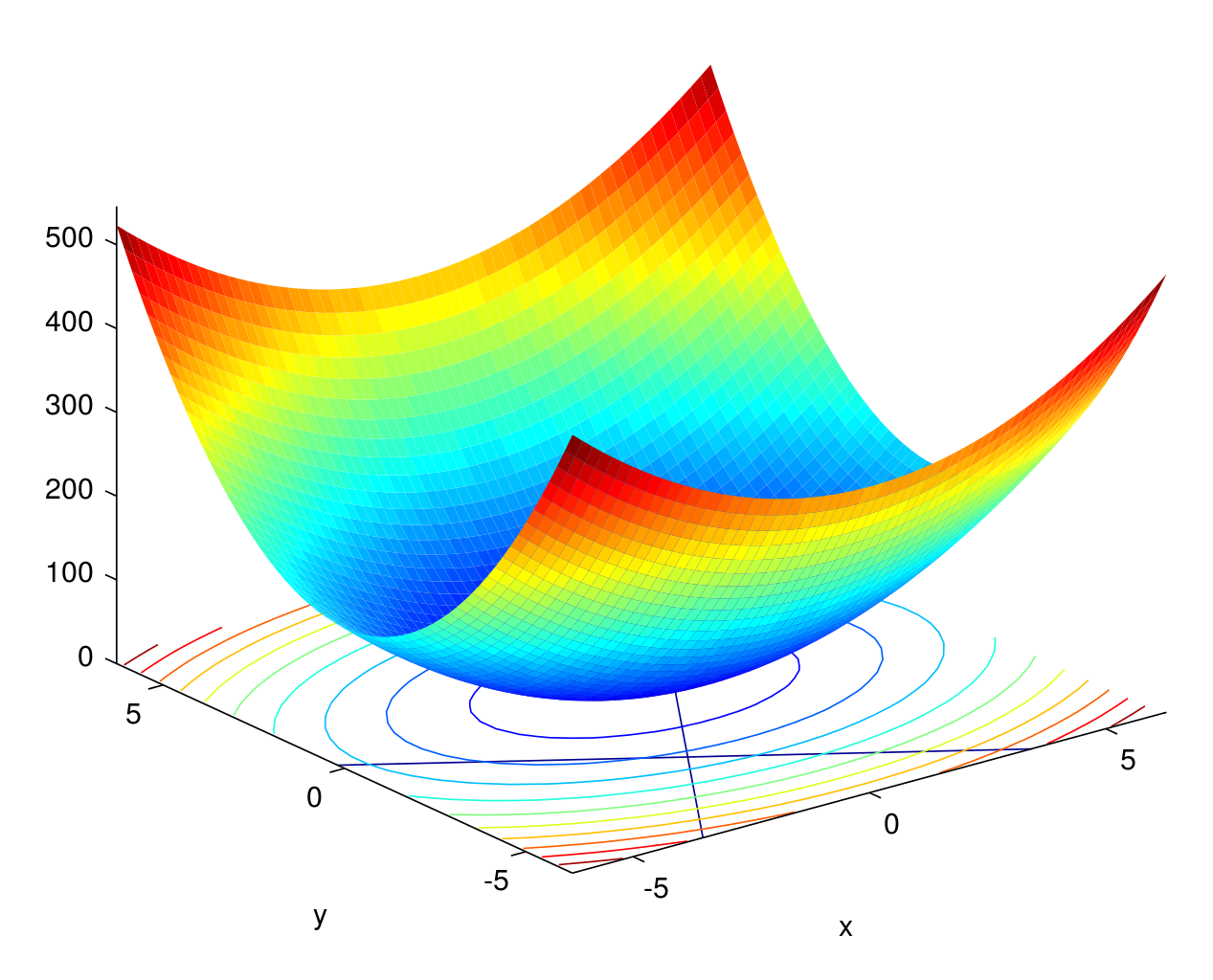
和单约束的解决方法类似,我们画出等高线图,目的就是在约束线上找到一个点可以和等高线相切,所得的值实在约束范围内的最大值或者最小值,直观表示如下图
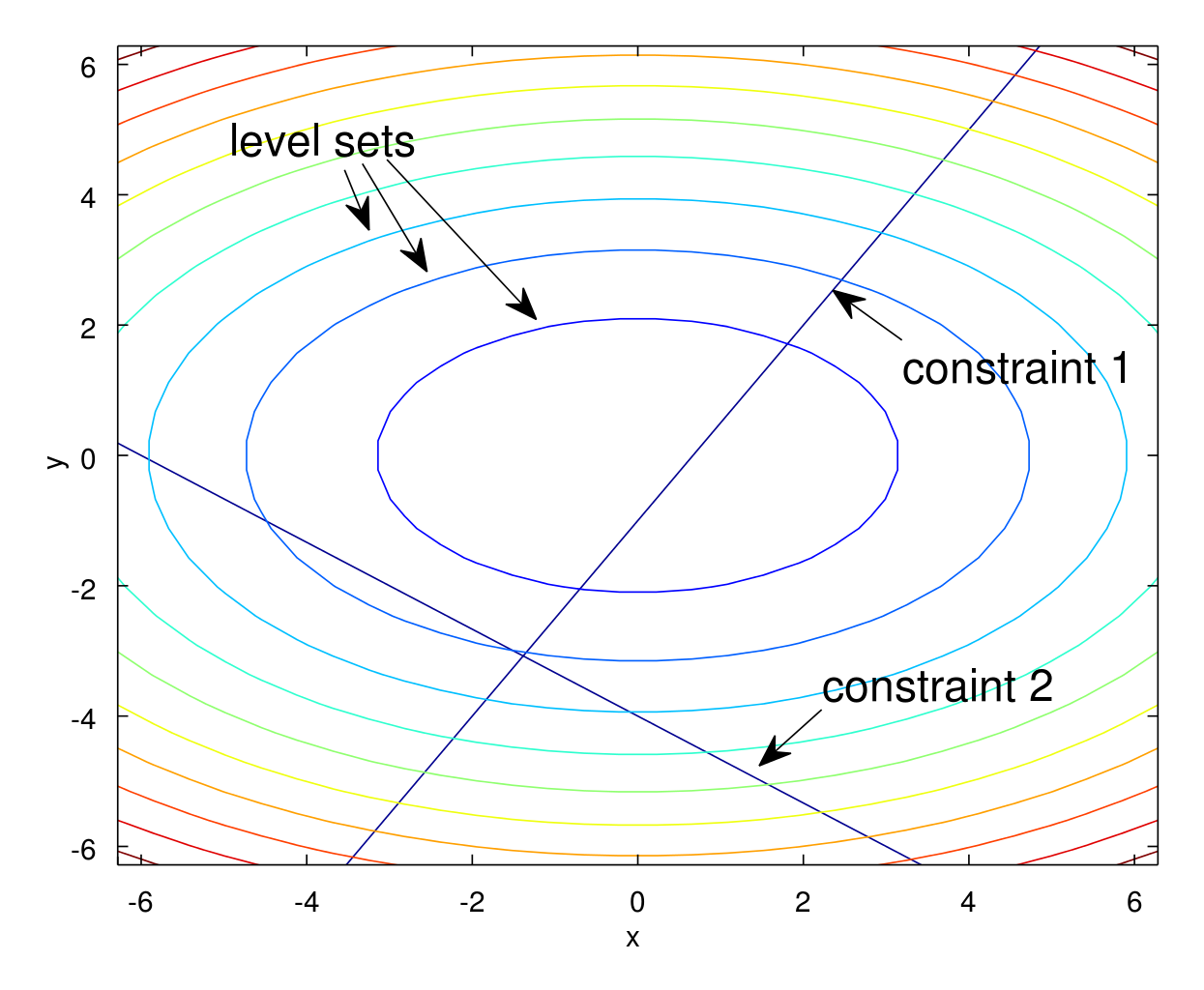
解算方法是讲单约束的扩展到多约束的情况,较为类似,可举一反三
KKT条件
已经解决的在等式约束条件下的求函数极值的问题,那不等式约束条件下,应该如何解决呢?
这就需要引出KKT条件(Karush-Kuhn-Tucker Conditions),它是在满足一些有规则的条件下,一个非线性规划问题能有最优化解法的一个必要和充分条件
考虑以下非线性最优化问题,含有 $m$ 个不等式约束,$l$ 个等式约束
$$
\operatorname*{min}_{x}f(x) \qquad s.t. \; g_i(x) \leqslant 0,\; h_j(x) =0
$$
必要条件
假设 $f,g_i,h_j$ 三个函数为实数集映射,再者,他们都在 $x^$ 这点连续可微,如果 $x^$ 是一个局部极值,那么将会存在一组称为乘子的常数 $\lambda \geqslant 0,\mu_i \geqslant0, \nu_j$ 令
$$
\lambda + \sum_{i=1}^m \mu_i + \sum_{j=1}^l |\nu_i| \gt 0, \\
\lambda \nabla f(x^*) + \sum_{i=1}^m \mu_i \nabla g_i(x^*) + \sum_{j=1}^l \nu_i \nabla h_j(x^*) = 0, \\
\mu_i g_i(x^*) =0 \; \text{for all} \; i=1,\ldots,m
$$
这里有一些正则性条件或约束规范能保证解法不是退化的(比如$\lambda$为0),详见
充分条件
假设 $f,g_i$ 为凸函数,$h_j$ 函数是仿射函数(平移变换),假设有一个可行点 $x^*$,如果有常数 $\mu_i \geqslant 0$ 及 $\nu_j$ 满足
$$
\nabla f(x^*) + \sum_{i=1}^m \mu_i \nabla g_i(x^*) + \sum_{j=1}^l \nu_i \nabla h_j(x^*) = 0 \\
\mu_i g_i(x^*) =0 \; \text{for all} \; i=1,\ldots,m
$$
那么 $x^*$ 就是全局极小值
总结
总的来说,拉格朗日乘子法是一个工具(手段或方法),来解决在有约束情况的求函数极值的问题
