【阅读时间】17min - 22min
【内容简介】从不同角度解释为何使用Logistic回归模型,解读模型的现实意义,详细解读为何使用以及什么是交叉熵损失函数。并详细梳理符号表达,对公式不再恐惧
什么是【回归(Regression)】
回归(Regression)是一项模拟技术,用来从一个或多个解释变量中预测输出变量的值
什么是及为什么【Logistic Regression】
回归(Regression)是用来预测的,比如给你一组虫子的腿长和翅膀长数据,让你判断虫子是A类虫还是B类虫。
逻辑回归则是用来预测二进制输出变量取值(如:是/不是)的预测技术
即输出变量只有两个值得预测技术
下文中将会从不同的角度
概率论角度
首先,需要回忆一下几个概念
【大数定理】
$$ \lim_{n\to\infty} \frac{1}{n} \sum_{i=1}^n {X_i} = \mu $$不断的采样一个随机变量,得到n个值,当n趋向于正无穷的时候,这个平均值就收敛于随机变量的期望
【中心极限定理】
大量相互独立{条件1}的随机变量,其均值的分布以正态分布{结论}为极限{条件2}
【贝叶斯公式】
默认你已经对条件概率了若指掌(在某件事情已经发生的情况下另一件事发生的概率),关于贝叶斯方法的前世今生,这个链接或许可以帮到你。
那贝叶斯公式是如何推出来的?
问题描述
我们需要求的问题是:你在校园里面随机游走,遇到了N个穿长裤的人(但是可能因为你高度近视你无法看出他们的性别),问,这N个人里面有多少个女生,多少个男生,即,穿裤子的人里面有多少个女生
解决过程
$$ 穿裤子的人中的女生比例 = \frac{穿长裤的女生人数}{穿长裤的总人数} =\\ \frac {U\times P(Girl)\times P(Paints|Girl)}{U\times P(Boy)\times P(Paints|Boy) + U\times P(Girl)\times P(Paints|Girl)}\tag{1-1} $$ 化简上式,可以发现其实分母合起来就是 $P(Paints)$ ,分子其实就是既穿裤子又是女孩,整理得 $$ P(Girl|Paints) = \frac{P(Girl) \times P(Paints|Girl)}{P(Paints)} $$再一般化,用A表示穿裤子的,B表示女生
$$
P(B|A) = \frac{P(B)\times P(A|B)}{P(A)} = \frac{P(AB)}{P(A)}\tag{1-2}
$$
上式就是贝叶斯公式的一般形式,我们在推导中发现,正常人类对频率的感知和理解速度要高于对概率的。
比如“穿长裤的女生人数”这个概念,用总人数乘以女人比例,得出女生人数,再用女生人数乘以女生中穿裤子人数的比例得到穿裤子的女生人数。这一串推导感觉毫无困难。但如果读成:在A发生条件下,发成B的概率,会让人乍看下,感到有一定的理解困难。
我们常说Sense,我觉得这就是一种敏感,对条件概率表达方式的敏感,在你看到的时候,抓住那个最关键的点,不存在任何的迷惑
那Logistic Function和贝叶斯公式有什么联系呢?
如果我们把公式(1-1)也符号化,$B_1$ 表示女生,$B_2$表示男生,$A$ 表示穿裤子
$$
P(B_1|A) = \frac {P(B_1)P(A|B_1)}{P(B_2)P(A|B_2) + P(B_1)P(A|B_1)}\tag{1-3}
$$
右边同时除以 $P(B_1)\times P(A|B_1)$ ,并定义 $a = \ln{\left( \frac{P(B_1)P(A|B_1)}{P(B_2)P(A|B_2)}\right)}$ 直接由公式(1-3)可得到
$$
f(a) = \frac{1}{1 + e^{-a}} \tag{1-4}
$$
很熟悉的形式,其实就是logistic函数的一般形式(对数几率函数),而这个函数的值就是 $f(a)$ ,很明显,是一个概率
另一个很重要超级重要的常识就是:正态分布的的累计分布函数(就是从负无穷到x积分)和概率分布函数长得样子很像Logistic累计分布函数和概率密度函数,可能看到这句话很多人就已经真相大白了,应给无论从中心极限定理出发,还是从统计学概率论角度来看,概率分布存在的价值是为了描述自然界(现实)中的随机事件,构造函数本身就十分重要,不同的规律需要不同的函数去拟合

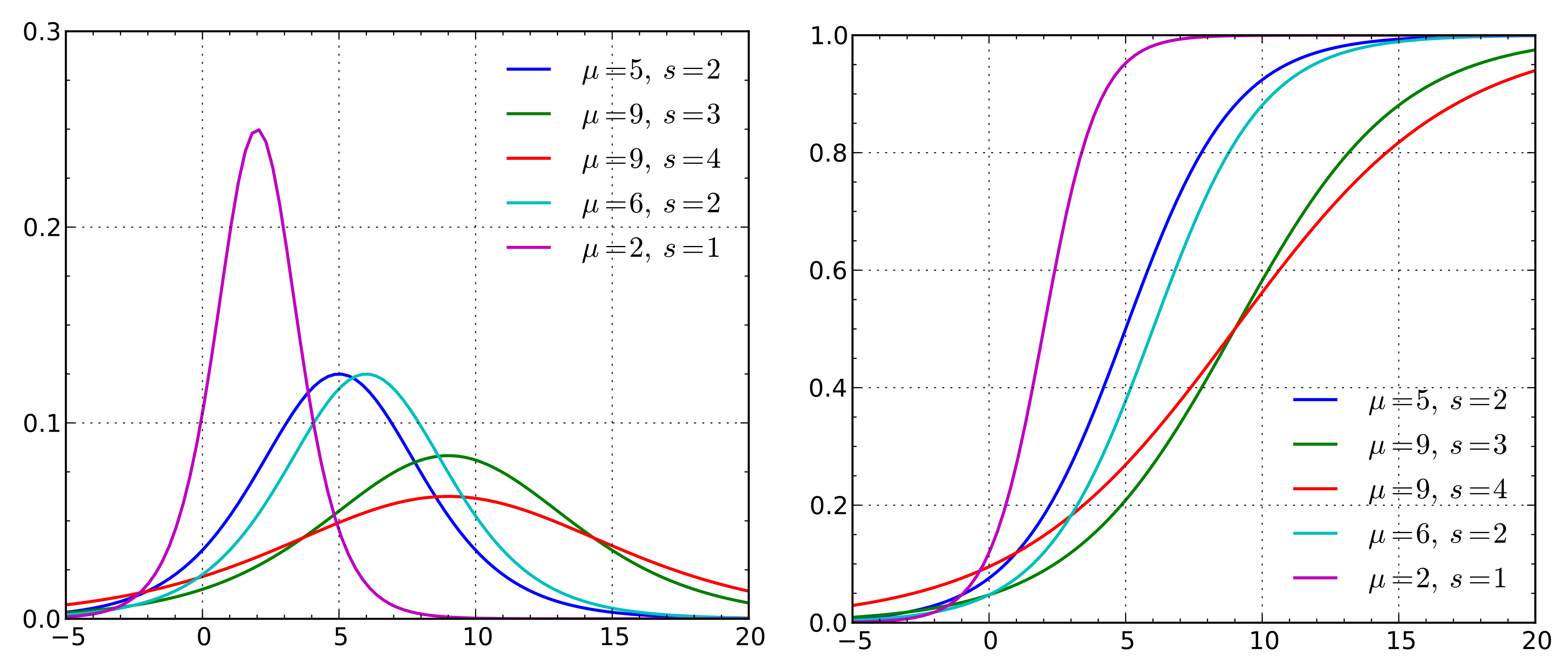
统计学角度
动机 - 需要解决什么问题
在现实生活中,有时候需要探究某一事件 $A$ 发生的概率 $P$ (0 - 1 之间的一个数)与某些因素 $\mathbf X = (X_1, X_2, \ldots, X_p)’$ 之间的关系。(其中1到p是各种不同的因素)
☆ 【核心问题】考虑到很多情况下,$P$ 对 $\mathbf X$ 的变化并不敏感,即 $\mathbf X$ 需要发生很大的变化才能引起 $P$ 的微弱改变
比如,农药的用量和杀死害虫的概率之间,在农药用量在很小的范围内增长的时候,因为药效不够,杀死害虫的概率增长很慢。
因此,我们要构造一个关于 $P$ 的函数 $\theta(P)$ ,使得它在 $P = 0$ 或 $P = 1$ 附近,$P$ 的微小变化对应 $\theta(P)$ 的较大改变,同时,$\theta(P)$ 要尽可能的简单。于是,我们可以构造一个函数(注意:构造函数是数学中很有效的手段,我们需要什么特性就用什么方法来构造一个满足我们需求的函数)c
$$
\frac {\partial \theta(P)}{\partial P} =\frac{1}{P} +\frac{1}{1-P}
$$
根据上述公式可以解得
$$
\theta(P) =\ln\left(\frac{P}{1-P}\right)
$$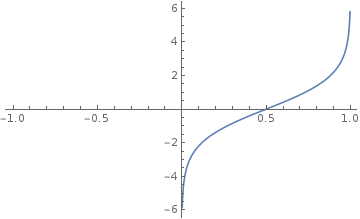
这个 $\theta(P)$ 就是Logit变换,可以看到,这个函数很符合我们的要求: $P = 0$ 或 $P = 1$ 附近,$P$ 的微小变化对应 $\theta(P)$ 的较大改变
方案 - 如何解决这个问题
为了建立因变量 $P$ 与自变量 $\mathbf X$ 之间的合理变动关系,一个很自然的假设就是线性关系,也就是:
$$
P = \mathbf X’ \boldsymbol{\beta}
$$
其中 $\boldsymbol \beta = (\beta_1,\beta_1,\ldots,\beta_p)$ 表示每一个不同因素对最终概率 $P$ 产生的影响(这个也可以写作,权重weight)
由需求可知,在某些情况下,$P = 0$ 或 $P = 1$ 附近,$P$ 对 $\mathbf X$ 的变化并不敏感,简单的线性关系不能反映这一特征。此时,构造的 $\theta(P)$ 就派上用场了
$$
\ln\left(\frac{P}{1-P}\right) = \mathbf X’ \boldsymbol{\beta}
$$
进行一系列的公式推导有
$$
\ln\left(\frac{P}{1-P}\right) = \mathbf X^\mathrm T \boldsymbol{\beta} \implies \frac{P}{1-P} = e^{\mathbf X^\mathrm T \boldsymbol{\beta}} \implies P = \frac{e^{\mathbf X^\mathrm T \boldsymbol{\beta}}}{1 + e^{\mathbf X^\mathrm T \boldsymbol{\beta}}}
$$
则上述最后推出的就是Logistic回归模型
机器学习角度
周志华《机器学习》,3.3 对数几率回归笔记
和统计学角度相同,我们的目的是依旧是完成一个二分类任务,输出标记 $y \in {0,1}$ ,而线性回归模型产生的预测值 $z = \boldsymbol w^{T}\boldsymbol x + b$ 是实值,于是,我们需要把 z 转换为0/1值,最理想的是单位阶跃函数(unit-step function z > 0➜y=1,z<0➜y=1)
单单位阶跃函数不连续,不能微分,积分,求逆,于是我们希望找到能在一定程度上近似单位阶跃函数的替代函数(surrogate function),并希望它单调可微,答案很明显,就是对数几率函数(logistic function)
$$
y = \frac{1}{1+e^{-z}}
$$
z 为预测值,y 为输出,对数几率函数是一种Sigmoid函数【一种形状类似S的函数】,将$z = \boldsymbol w^{T}\boldsymbol x + b$ 带入上面的公式
$$
y = \frac{1}{1+e^{-(\boldsymbol w^{T}\boldsymbol x + b)}} \implies \ln(\frac{y}{1-y}) = \boldsymbol w^{T}\boldsymbol x + b
$$
如果将 $y$ 作为 $\mathbf x$ 作为正例的可能性,$1-y$ 为其反例的可能性
$$
\frac {y}{1-y}
$$
上面的式子成为“几率”(odds):表示 $\mathbf x$ 是正例的相对可能性,对odds取对数得到“几率对数”(log odds,也就做logit)
生态学角度
可以换一个角度来解读这个问题的前世今生
1798年的时候一个叫Malthus的英国牧师发现人口的变化率和人口的数目成正比,需要用数学的手法建立一个公式来表征这个现象,则,使用 $N(t)$ 这个函数来表示t时刻某个地区的总人口数(根据成正比)
$$
\frac{dN(t)}{dt} = {rN(t)}
$$
其中,
r是常数,表示 $N(t)$ 的变化率
直接解出这个方程
$$
N(t) = N_0e^{rt}
$$
这很明显是一个指数增长函数,其实也是种群增长的函数表示
但是问题也是很明显的:种群因为环境容量的限制一定是不能无限增长的,即,这个模型非常不靠谱,需要重新设计模型来复合现实中的情况。Pierre-François Verhulst 在1838年提出,构造一个函数
$$
\frac{dN(t)}{dt} = {rN(t)}\left(1 - \frac{N(t)}{K}\right)
$$
K是一个常数,表示系统的容量(capacity)
令 $f(t) = \frac{N(t)}{K}$ ,在方程两边同时除以 $K$ ,上述方程变为:
$$
\frac{df(t)}{dt} = rf(1 - f)
$$
这也是Logistic方程的一般形式
总结
从不同的角度来研究问题就会发现,其实很多时候我们解决一个问题具有一个相似的模式,包括大数定律,贝叶斯全概率公式是一切的基石和解决问题的主要工具
一个模型的建立规则依据数据的分布特征,而这里依托的一个关键信息就是:在靠近输入0,1两点的时候,y随x的变化不明显,线性模型没法很好的反应这个特征,所以就构造了一个逻辑回归模型来表示这个特征
并且Logistic回归模型的本质是一个概率模型,因为在描述该分类时,我们其实是以概率来衡量的
重要概念
均方误差 Mean Squre Error MSE
指参数估计值与参数真值之差平方的期望值,是一种目标函数(Objective Function),常用于线性回归
$$
MSE = \frac{1}{n} \sum_{t = 1}^n{(observed_t - predicted_t)}^2
$$
交叉熵 Cross Entropy
又称为logloss,是Objective function的一种,也称Loss function or Coss Function
什么是熵
我觉得这个问题必须搞明白一件事就是:什么是熵 Entropy
- 广义的定义是:熵是描述一个系统的无序程度的变量;同样的表述还有,熵是系统混乱度的度量,一切自发的不可逆过程都是从有序到无序的变化过程,向熵增的方向进行
- 有一个很神奇的解释是:熵字为火字旁加商。当时有位姓胡的学者作为普朗克的防疫。S(entropy)定义为热量Q与温度的比值,所以造字:熵
- 至于信息论上熵的概念更有意思,有兴趣可以转到
要理解这个Cross Entropy,必须了解它是用来干啥的?
延伸:信息熵 交叉熵 相对熵的理解,需要跳转到另一篇笔记:什么是信息熵、交叉熵和相对熵
简单来说Cross Entropy可以表示可以度量最终训练结果于测试集的差异程度,MSE也是同样的作用。
换种更具体的说法:我们用p表示真实标记(训练样本标记)的分布,q是训练后的模型的预测标记(输出值标记)的分布,而交叉熵损失函数可以衡量p与q的相似性。
似然函数
定义:给定联合样本值 $x$ 关于(未知 - 因为也是一边的自变量)参数 $\theta$ 的函数
$$
L(\theta|x) = f(x;\theta)
$$
$x$ 指联合样本随机变量 $X$ 取到的值,比如天气取值 $X$ =【晴,阴,雨,雪】$x$ = 晴
$\theta$ 指未知参数,属于参数空间,比如正态分布的均值,方差等
$f(x;\theta)$ 是密度函数,表示 $\theta$ 参数下联合样本值 $x$ 的联合密度函数(所以这里不用|符号,|符号表达的意思是条件概率或条件分布)
从定义上,似然函数和密度函数是完全不同的两个数学对象:前者是关于 $\theta$ 的函数,后者是关于 $x$ 的函数。中间的等号理解成函数值形式相等
这个等式表示的是对于事件发生的两种角度的看法。左边表示概率,右边表示可能性。要表达的含义都是:给定一个样本 $x$ 后,我们去测度这个样本出现的可能性到底有多大。说人话,比如样本空间是 $X =【晴,阴,雨,雪】$,函数表达的就是样本 $x$ = 晴在这个样本空间下发生的概率或可能性
从统计学的角度来说,这个样本的出现一定是基于一个分布的(比如二项分布,只正态分布等等),那么我们假设这个分布为 $f(x;\theta)$ ,对于不同的 $\theta$ 样本的分布不一样。
$f(x;\theta)$ 函数表示的就是在参数 $\theta$ 下 $x$ 出现的概率有多大(可以带入天气例子思考)
$L(\theta|x)$ 表示在给定样本 $x$ ,哪个参数 $\theta$ 使得 $x$ 出现的可能性有多大。说人话,我们已经知道天气是晴天,哪个参数(可能是 $\theta_1$ $\theta_2$)使得这个函数值最大
对于Logistic Regression 为什么要用LogLoss - Cross Entropy
了解了熵,和似然函数,我们可以开始看看在Logistic Regression的条件下为什么要用LogLoss,换句话也就是说,它一定有它的优势,我们采用,那么它有什么优势?
Logistic Regression的本质还是一个二分类问题,即Y = 0,or Y = 1
令 $P(Y=0|x) = \pi(x)$ $P(Y=1|x) = 1 - \pi(x)$
$y_i$ 表示i次试验,取值就是0 or 1(二分类问题)
$\pi(x) = \frac{1}{1 + e^{-wx}}$ 是Logistic Function的表现形式,其中w相当于似然函数一节提到的 $\theta$ 是需要求的参数(加深理解,其实在二分类问题中,Logistic函数就是一种形式上的概率分布的表现形式)
所以使用基本概率方法可以求解二分类的问题的似然函数
$$
\ell(w) = \prod_{i = 1}^{N} [\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}
$$
注解:说白就和算扔N次硬币,一个连续正反事件串的概率是多少一个含义
看到乘法和指数,第一反应取对数,得到对数似然函数
$$
L(w) = \sum_{i=1}^N{[y_ilog_a\pi(x_i) + (1-y_i)log_a(1-\pi(x_i))]}
$$
如果跟随我的步伐走到这一步,你会发现,这个形式,前半部分是“正例成立”的交叉熵,后半部是“反例成立”的交叉熵,说实话,叫做交叉熵和二项分布,伯努利过程分不开联系。在上面不远的地方已经详细定义了这几个符号代表的意思
我们发现,$-\frac{L(w)}{N}$ 就是我们一直使用的Objective function or Loss Function or Cost Function(加负号才是最终的形式)。总之,训练的目的就是要求能够使得这个函数达到最小的参数,最终的目的还是计算出模型参数,就是 $w$ ,这个参数在上方的统计学角度,和机器学习角度都进行的讨论,重复阅读可以链接这些知识点
至于LogLoss的好处,一是取对数之后,乘法边加法,指数放下来,是凸函数,方便可以寻找最优解。二是加快了收敛速度,这里有个形象的步长比喻,可以想象成去了对数后,缩小了尺度,可以让最快梯度下降法要走的距离变短
